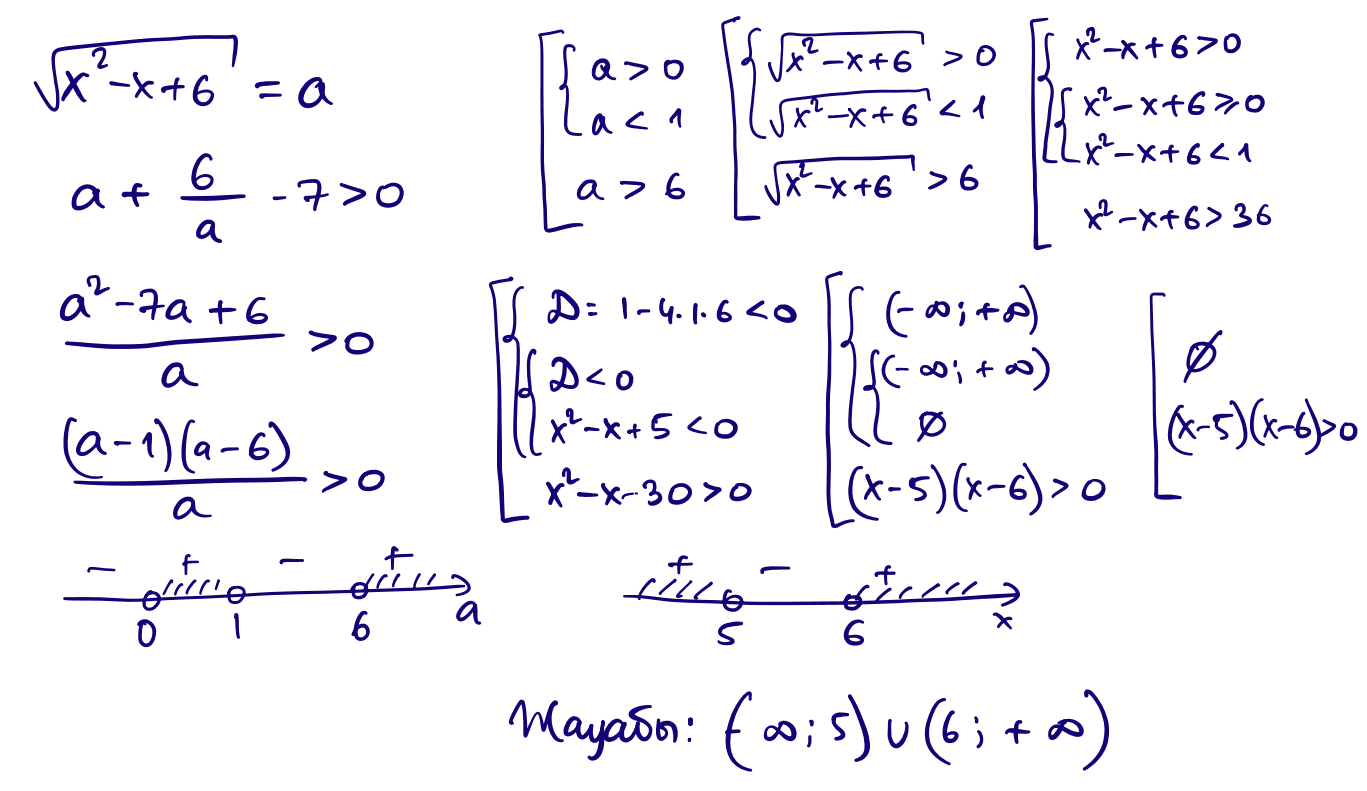1) $\dfrac{2-\sqrt{x+2}}{1-\sqrt{x+2}}\le 0$
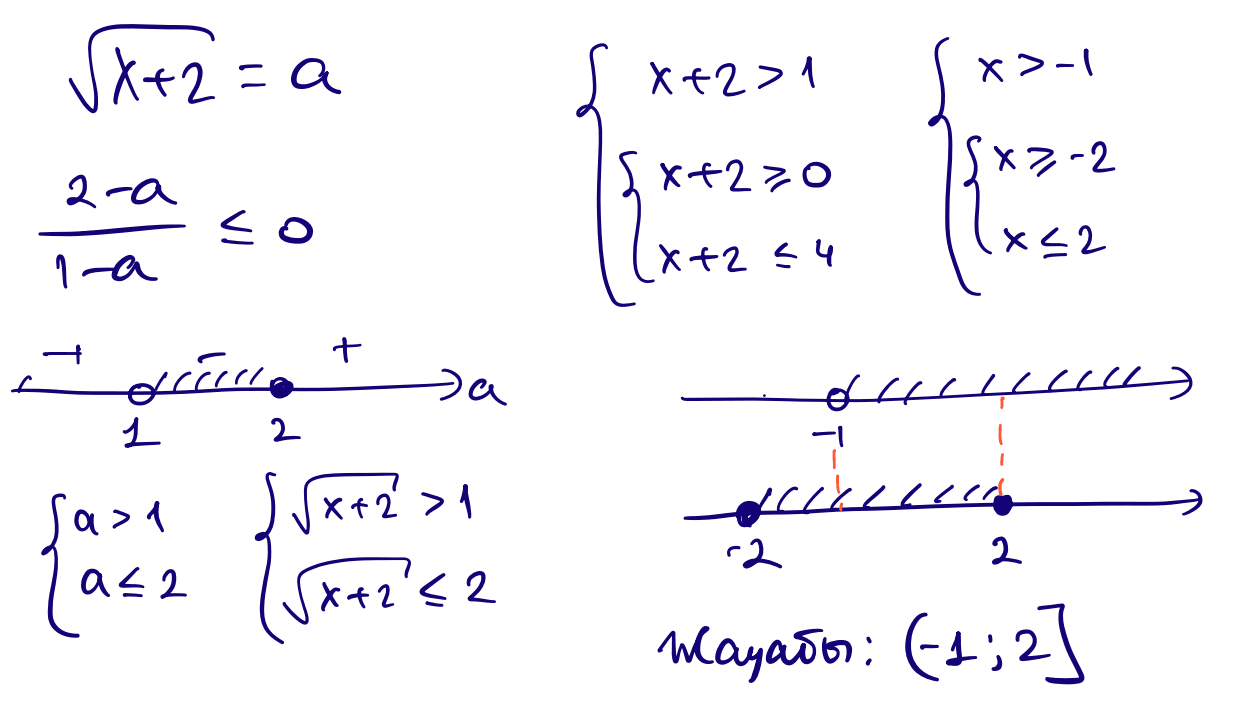
2) $\sqrt{x}-3\le\dfrac{2}{\sqrt{x}-2}$
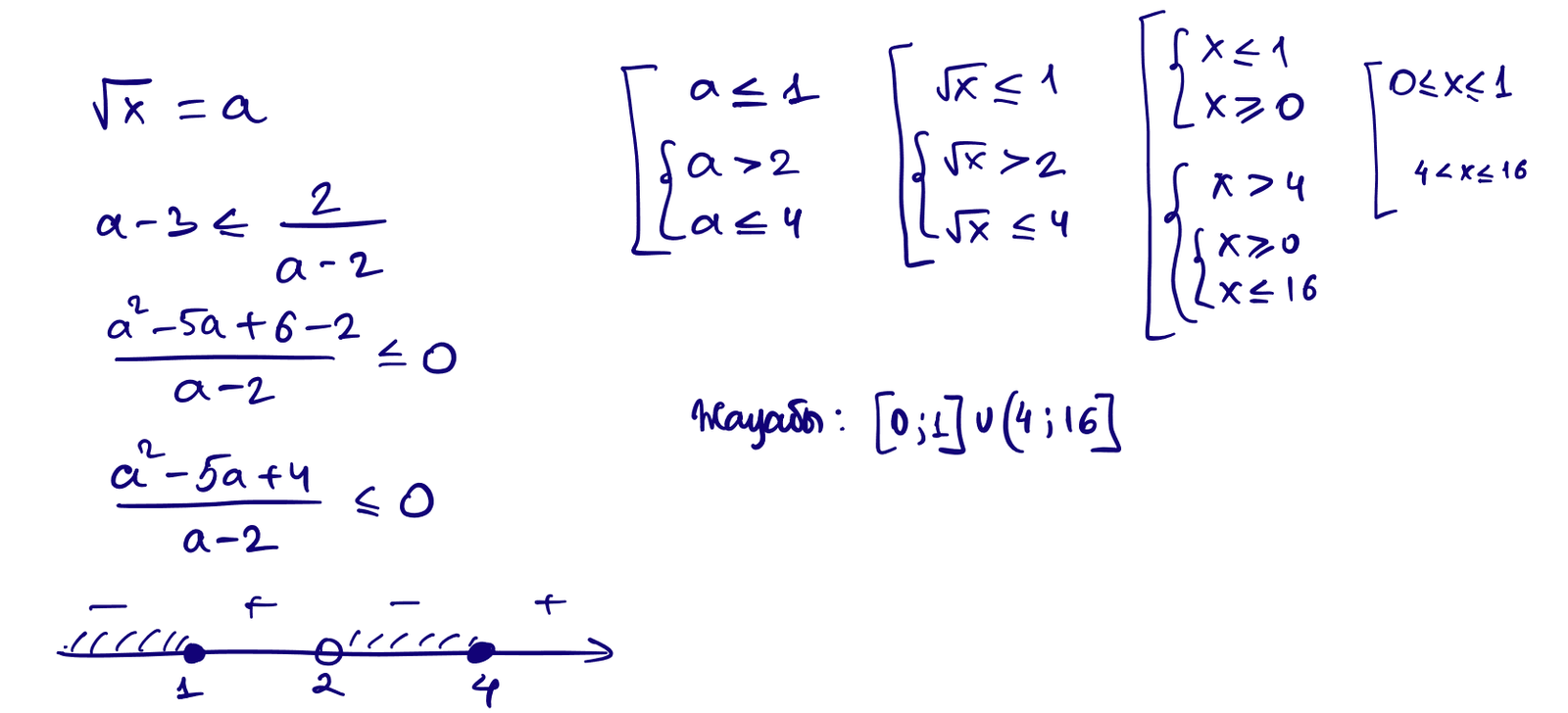
3) $x^2+\sqrt{x^2+11}-31\lt 0$
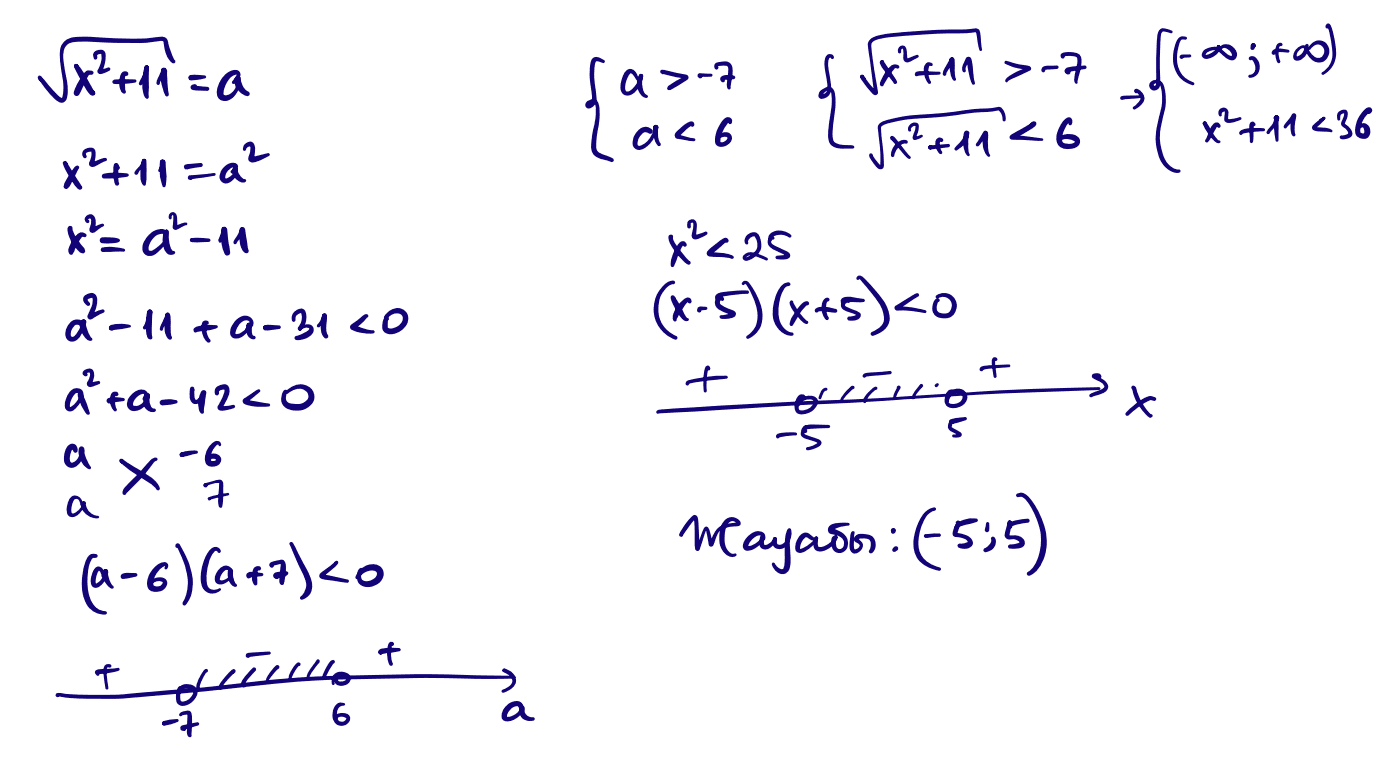
4) $2\sqrt{x}+\dfrac{1}{\sqrt{x}}\lt 3$
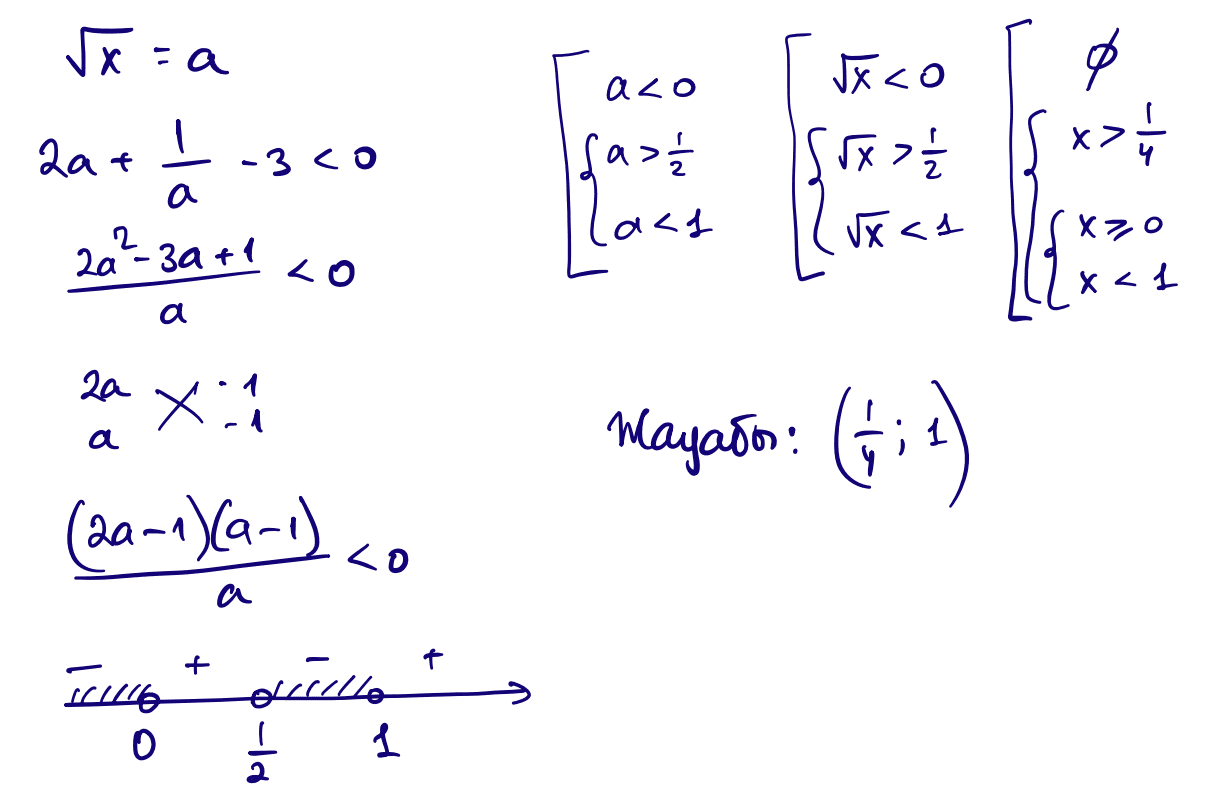
5) $\dfrac{x-\sqrt{x}-2}{x-\sqrt{x}-6}\gt 0$
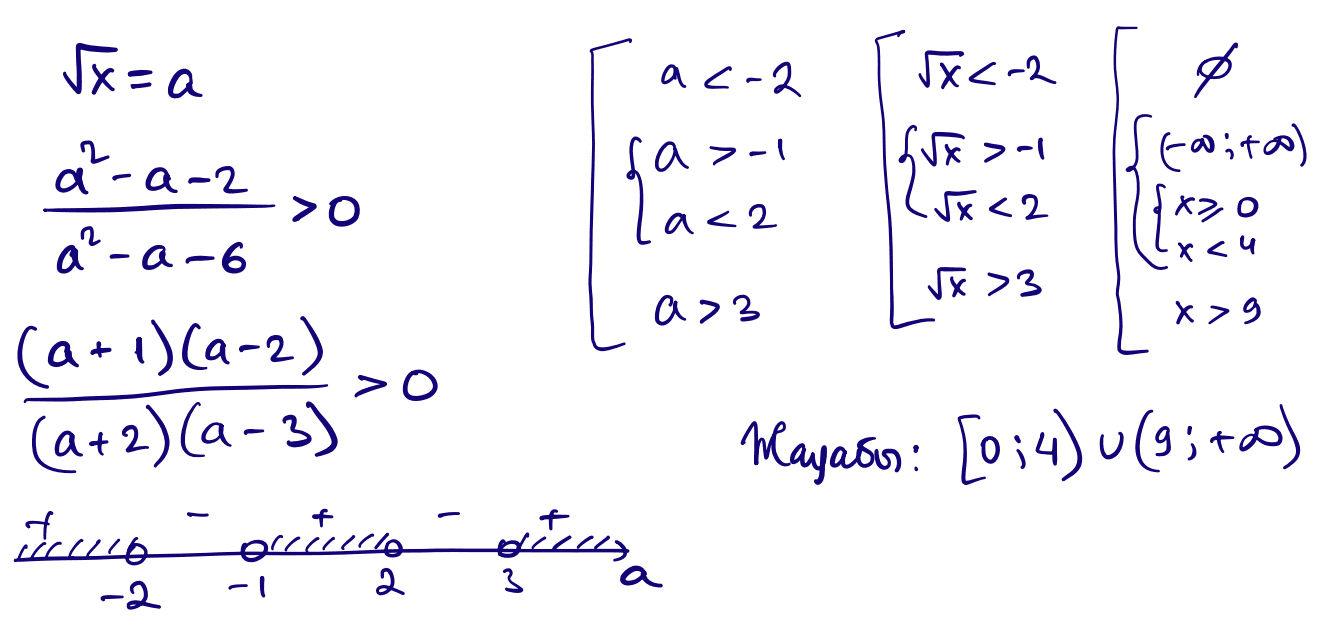
6) $3\cdot\sqrt[3]{x+1}-\sqrt[3]{x+1}\ge 2$
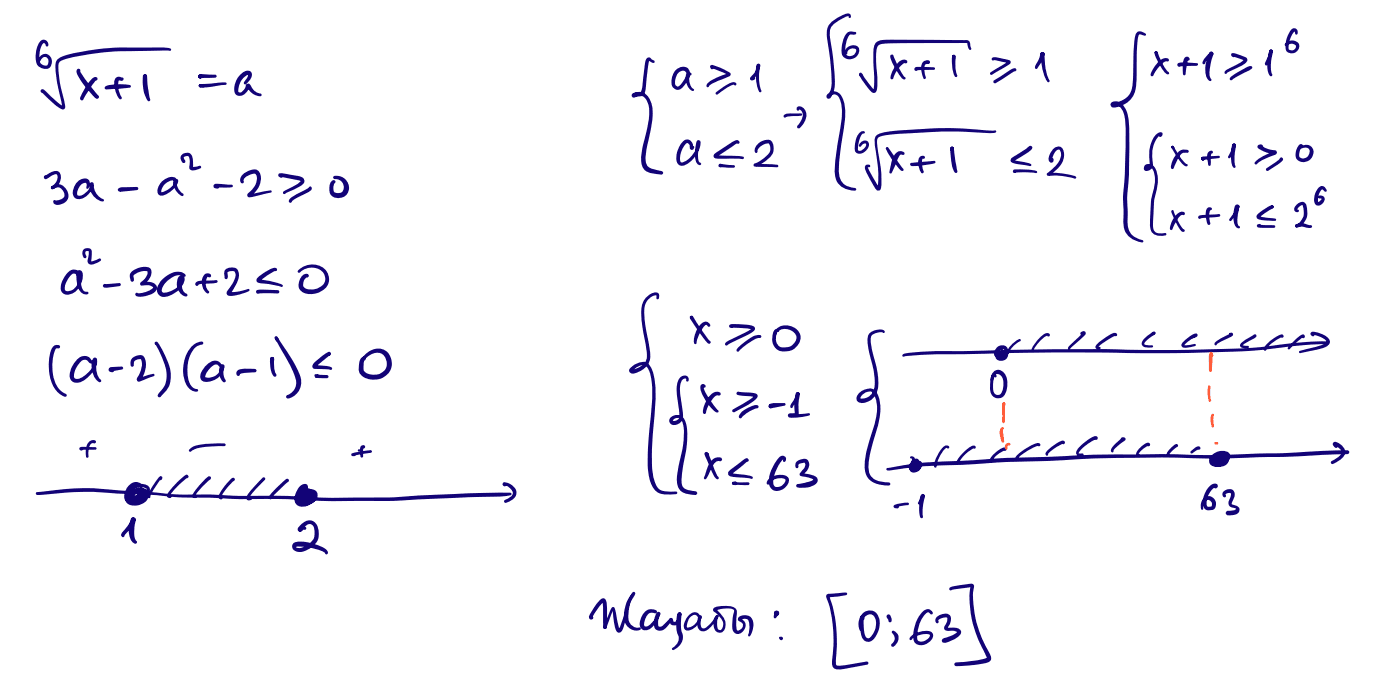
7) $\dfrac{\sqrt{x+3}-1}{5-\sqrt{x+3}}\ge 0$
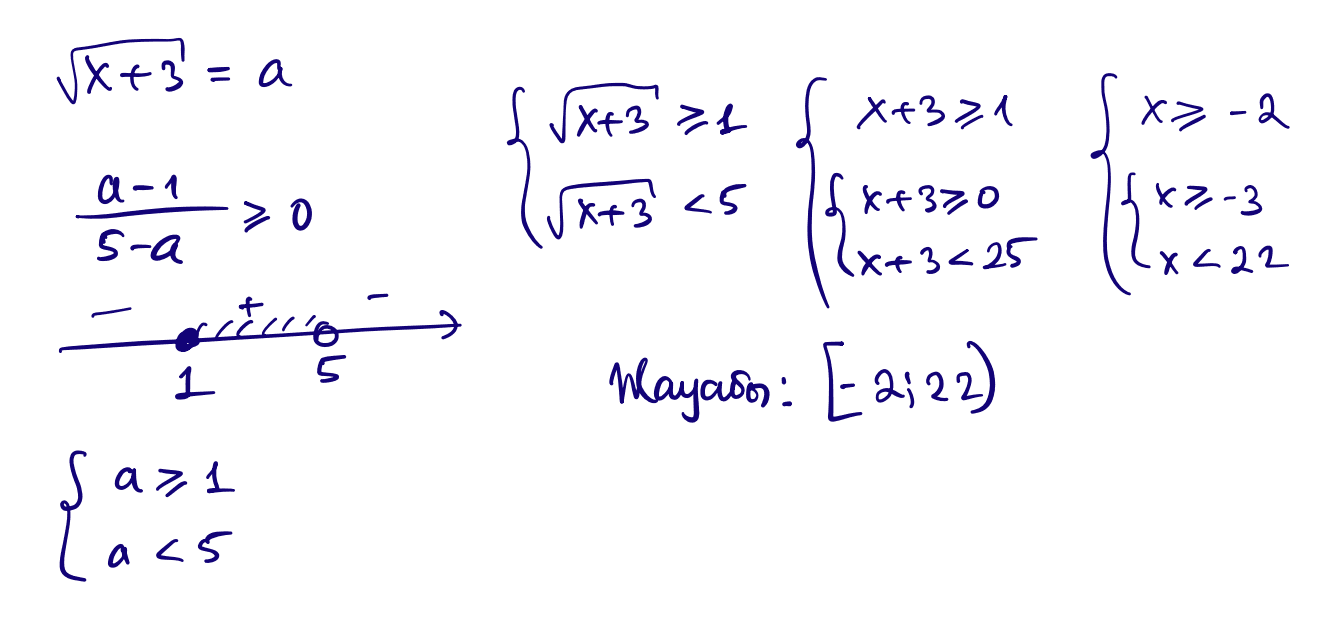
8) $\sqrt{1-x}+\dfrac{1}{\sqrt{1-x}}\gt 2$
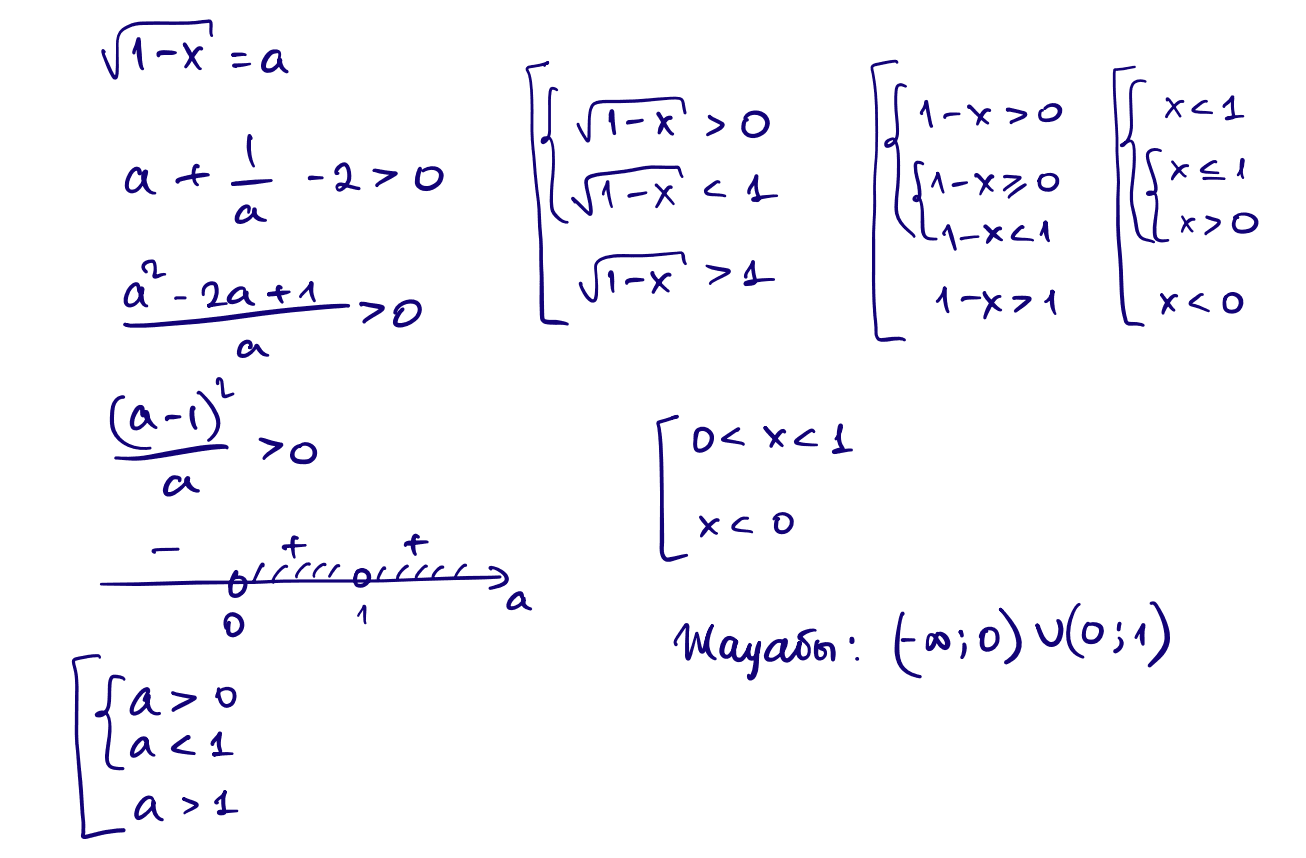
9) $x-5\sqrt{x}\le 6$
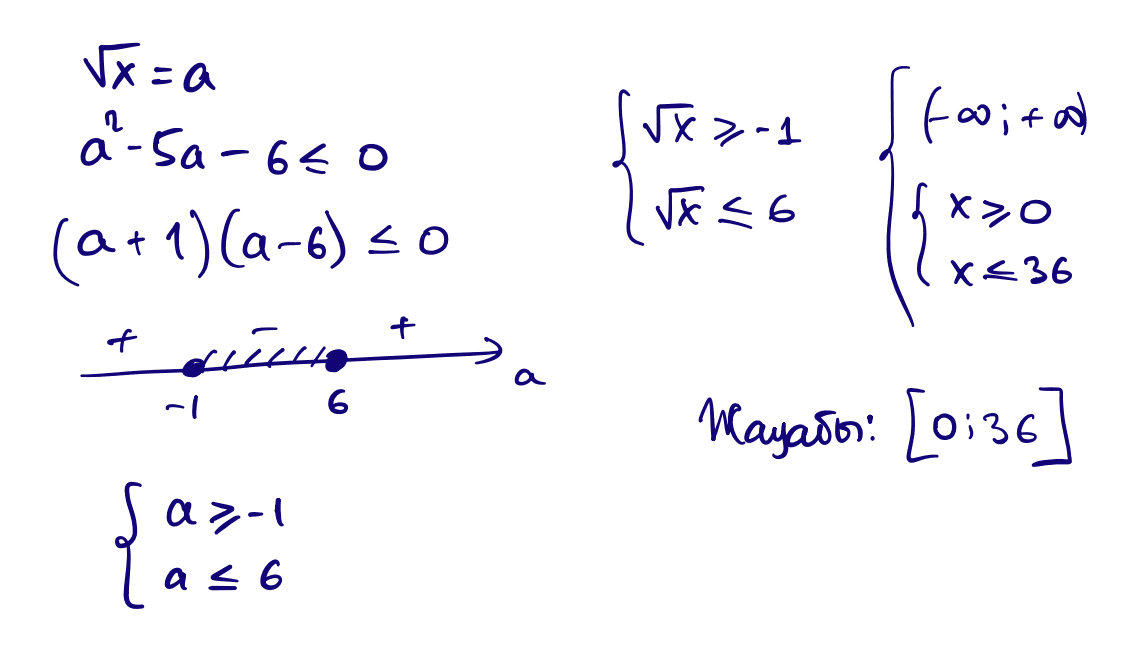
10) $\dfrac{\sqrt[3]{1-x}-2}{\sqrt[3]{1-x}+3}\ge 0$
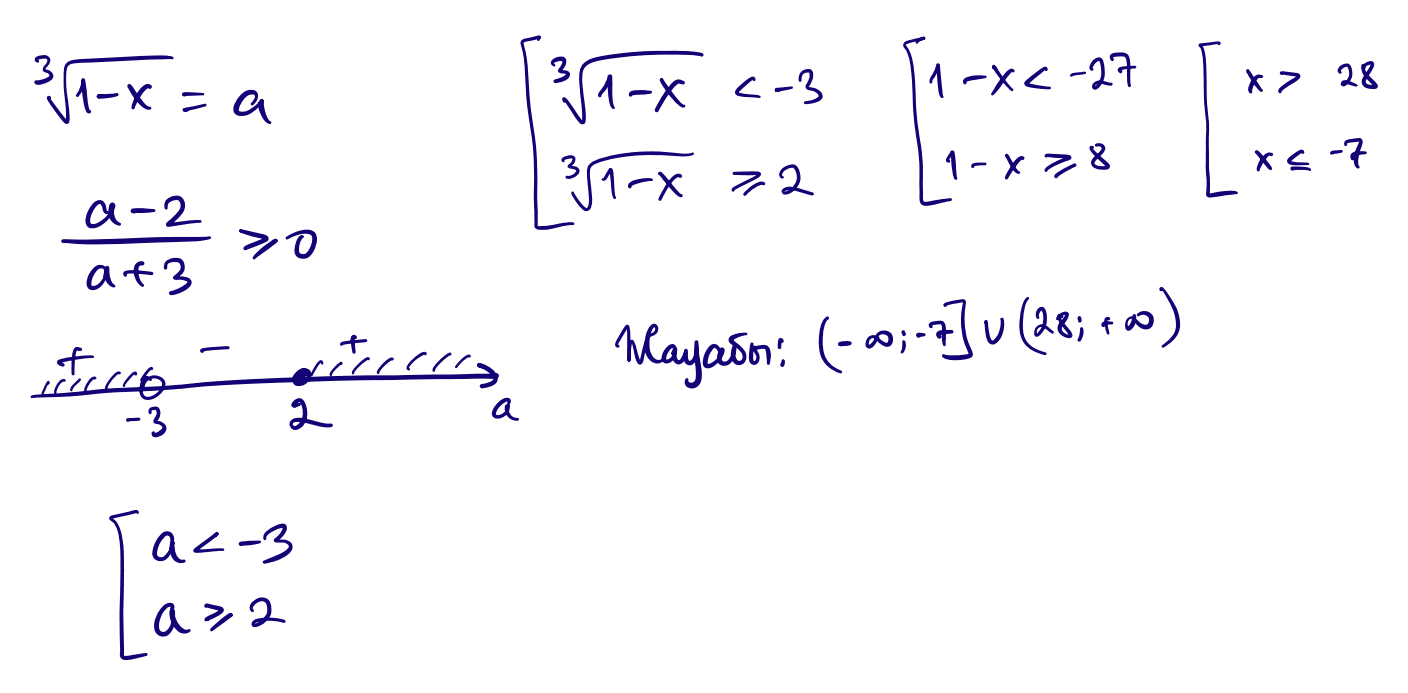
11) $\dfrac{2x+1}{x}-2\cdot\sqrt{\dfrac{2x+1}{x}}\ge 3$
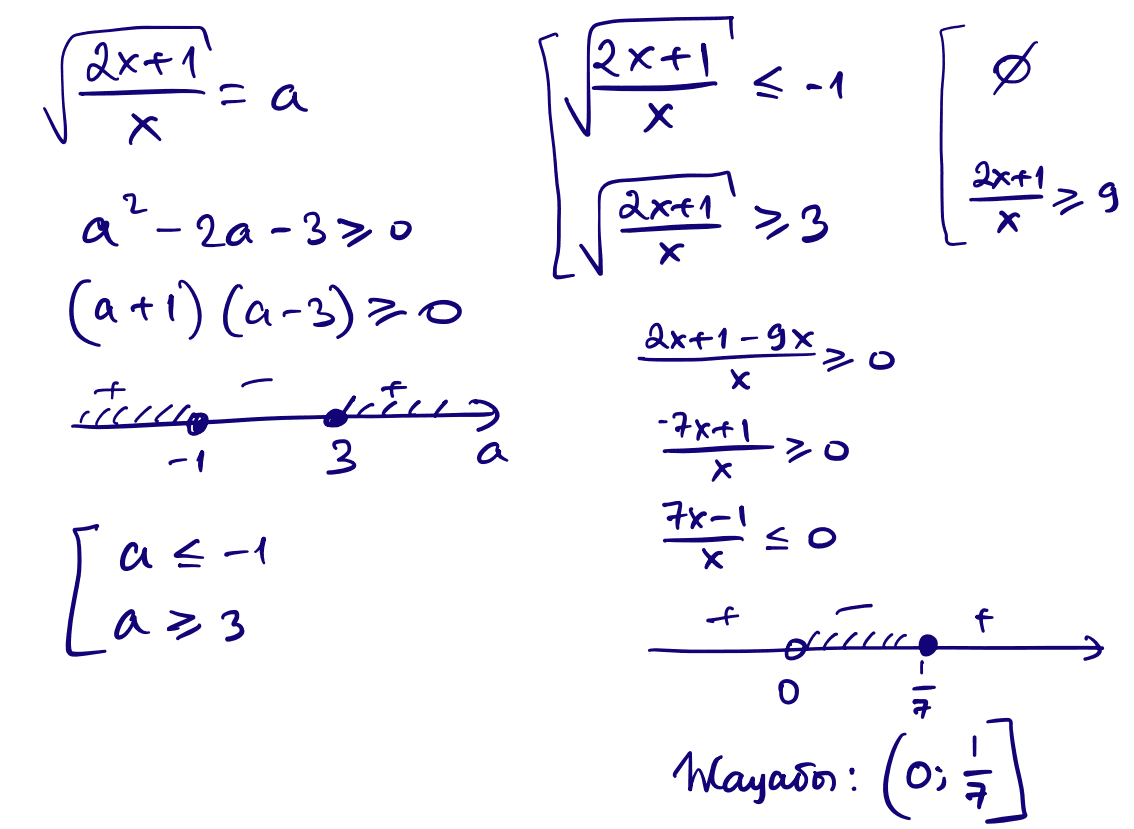
12) $x^2-3\sqrt{x^2-4x+20}\ge 4x-10$
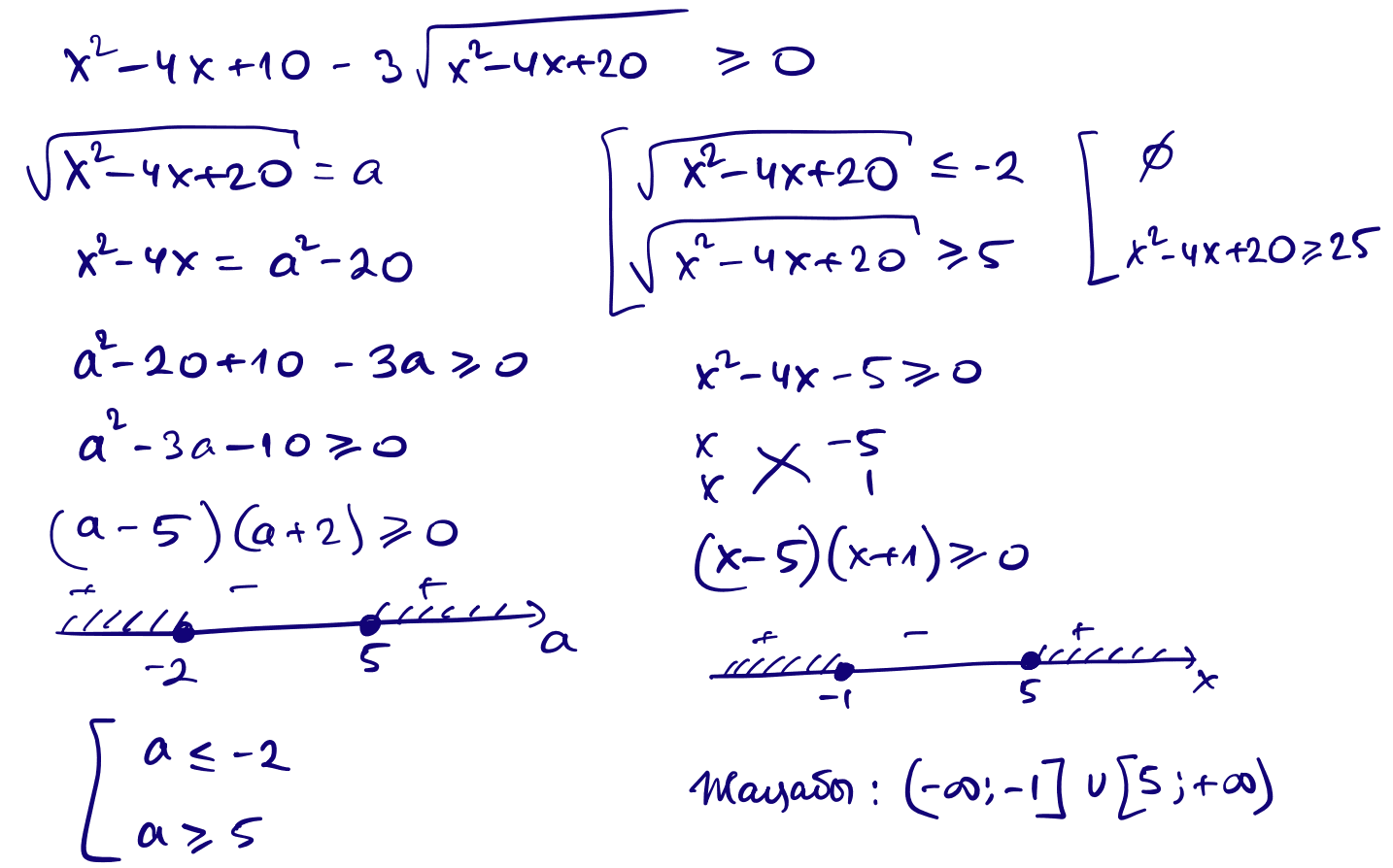
13) $(x+5)(x-2)+3\sqrt{x(x+3)}\gt 0$
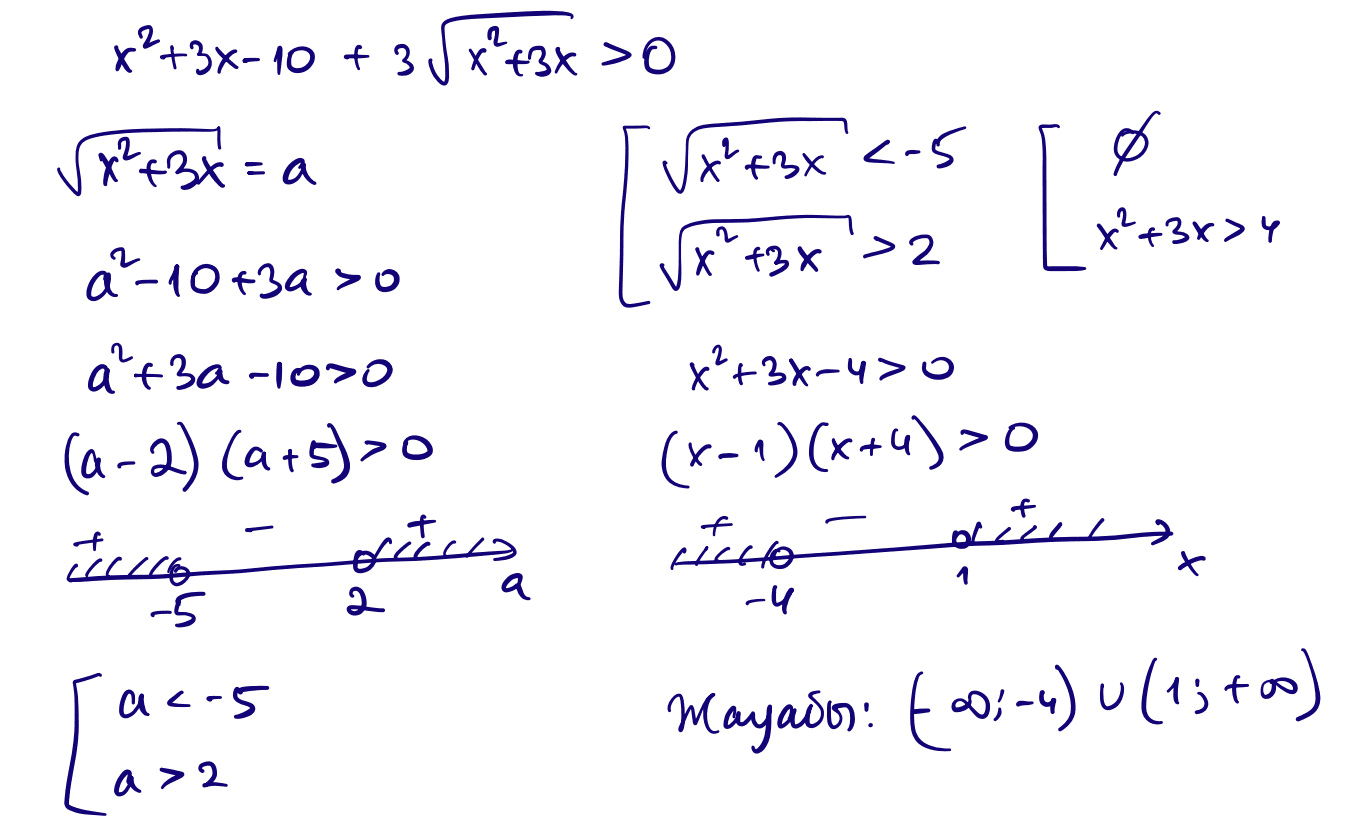
14) $x^2+5x+4\lt 5\sqrt{x^2+5x+28}$
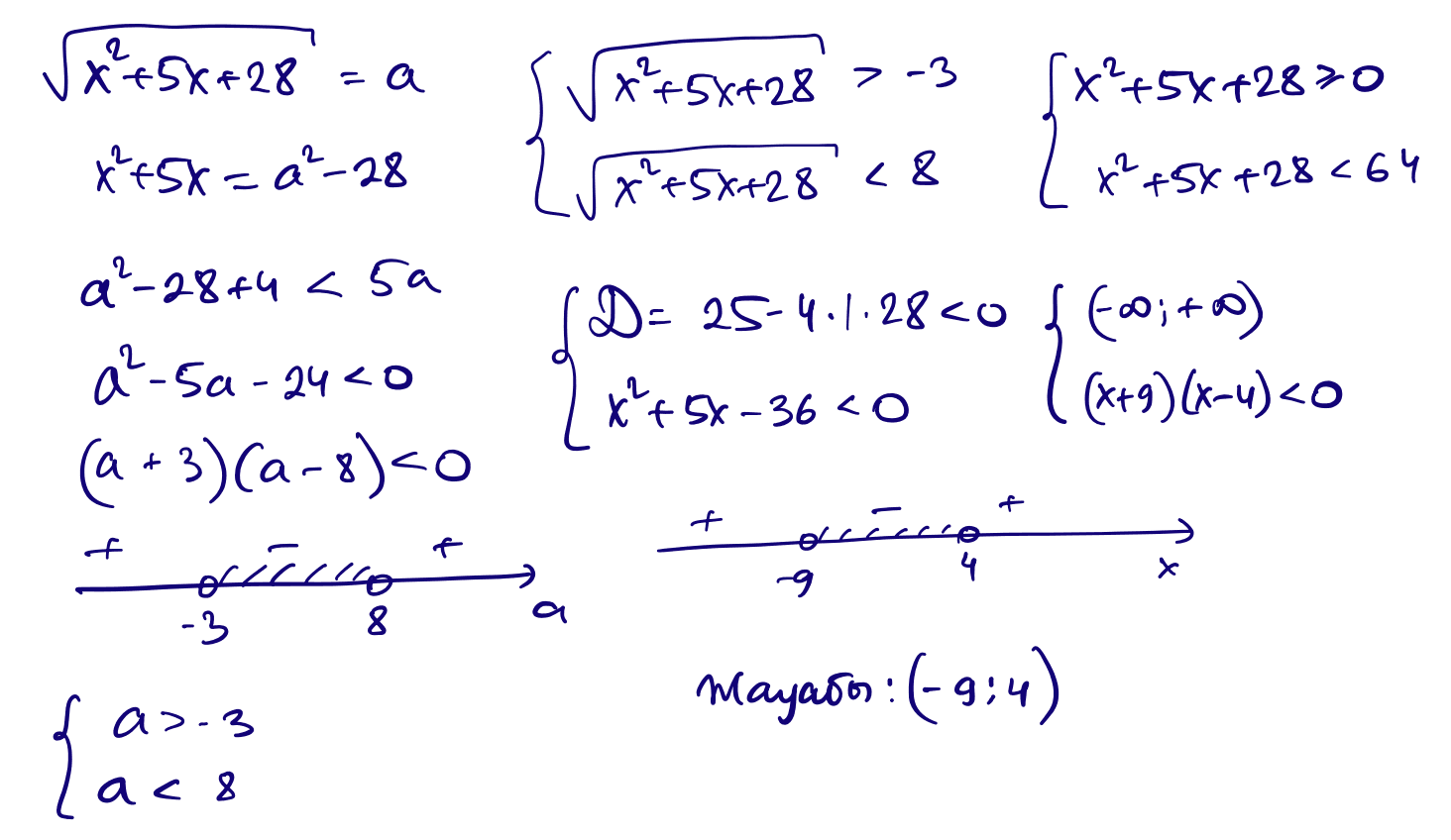
15) $\sqrt{x^2-3x+5}+x^2-3x-7\le 0$
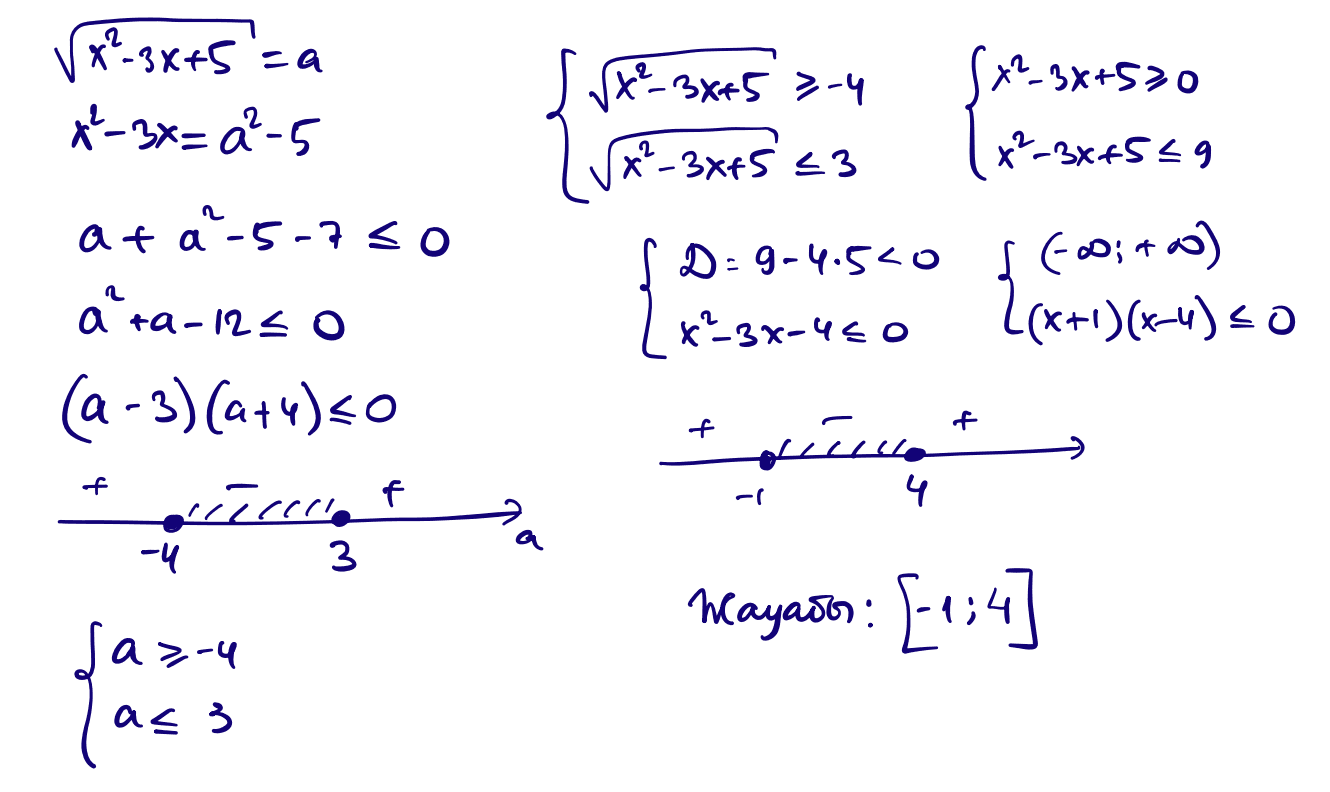
16) $\sqrt{x^2-x+1}+x^2-x-1\gt 0$
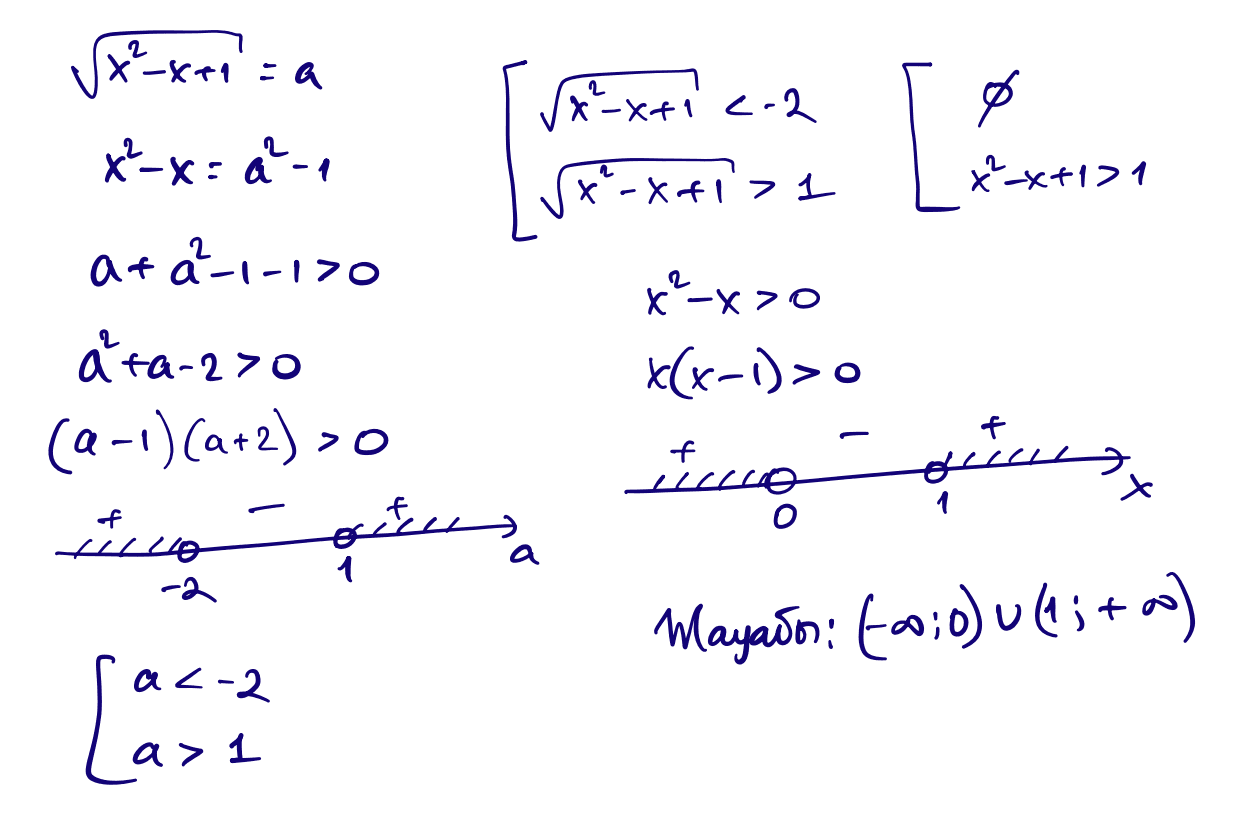
17) $\dfrac{x}{2-x}-\dfrac{3}{4}\sqrt{\dfrac{x}{2-x}}\le\dfrac{1}{4}$
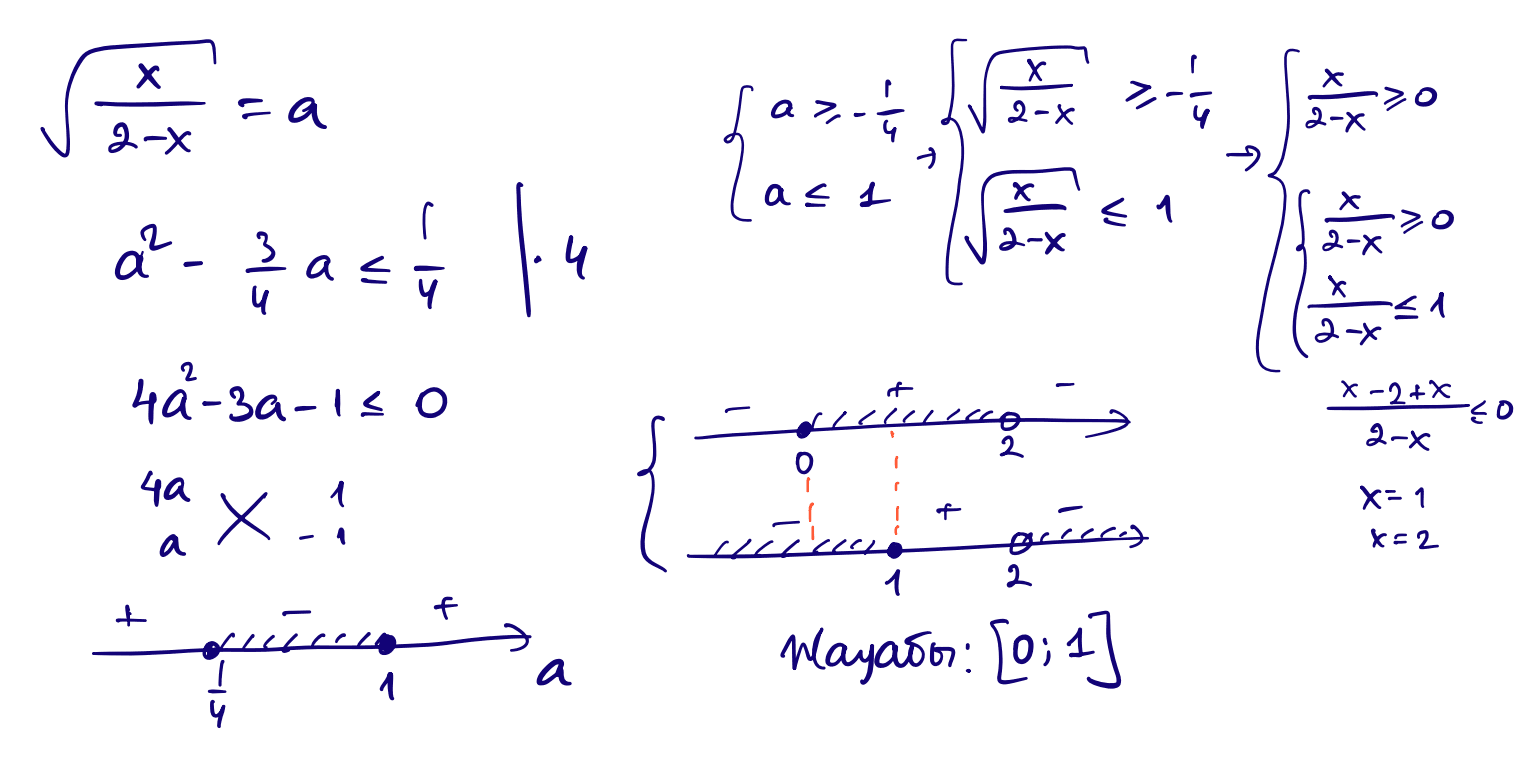
18) $\dfrac{1}{1-\sqrt{x}}\le\dfrac{1}{2\sqrt{x}+1}$
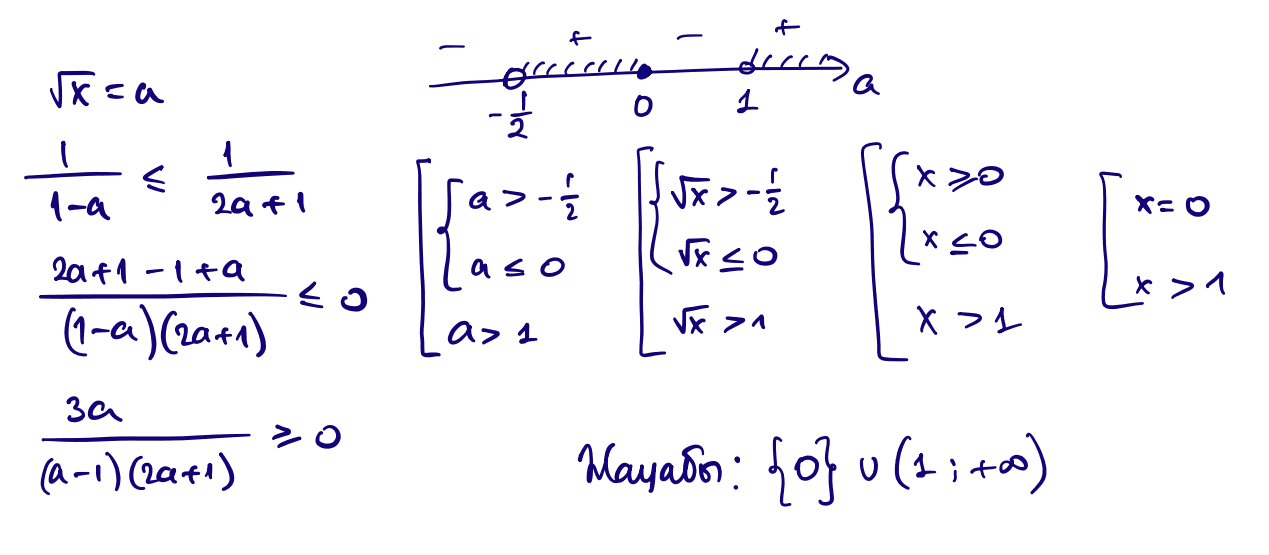
19) $\sqrt{x^2-x}\lt\dfrac{6}{\sqrt{x^2-x}}$
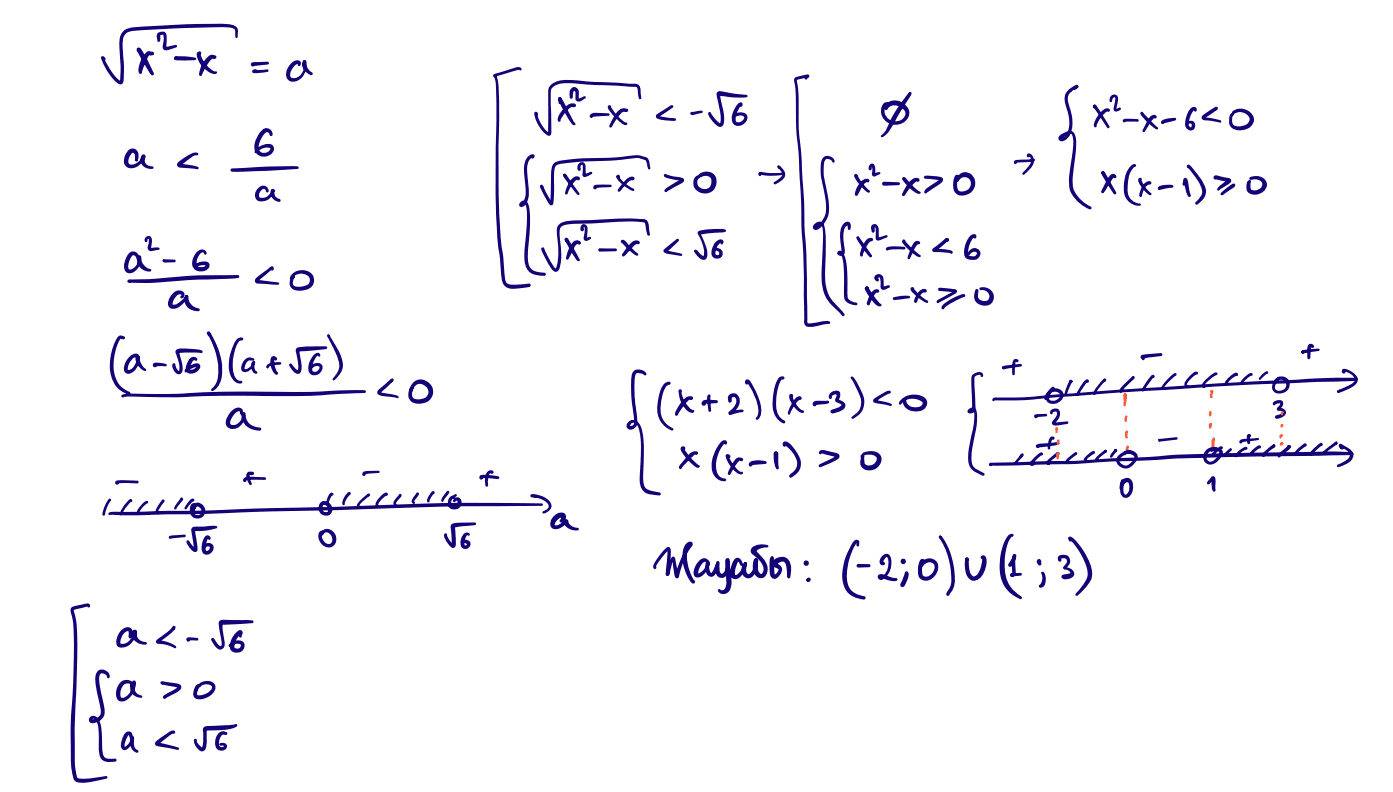
20) $\sqrt{x^2-x+6}+\dfrac{6}{\sqrt{x^2-x+6}}\gt 7$