8.1.1. Кез келген үшбұрыш тақырыбына берілген есептер

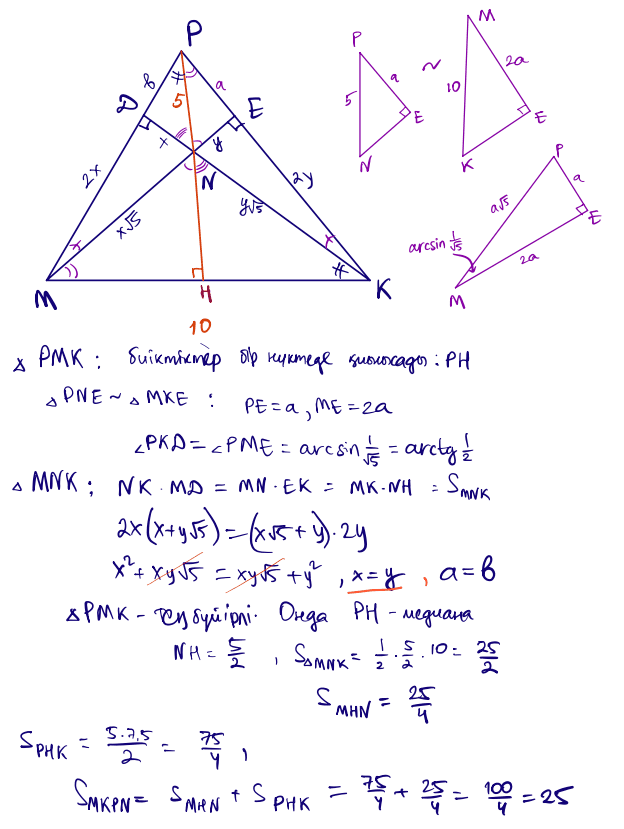
№ 1 Қабырғаларының ұзындықтары 4 және 6, ал олардың арасындағы бұрышының тангенсі 0,75-ке тең екендігі белгілі болса, үшбұрыштың ауданын табыңыз.

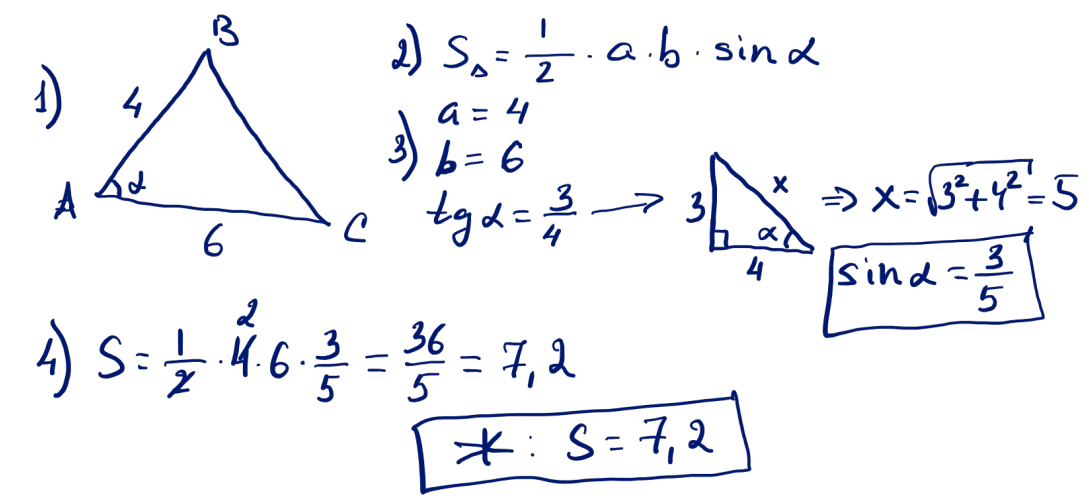
№ 2 Үшбұрыштың табаны 60, биіктігі 12, ал табанына жүргізілген медианасы 13-ке тең. Үшбұрыштың үлкен бүйір қабырғасын анықтаңыз.

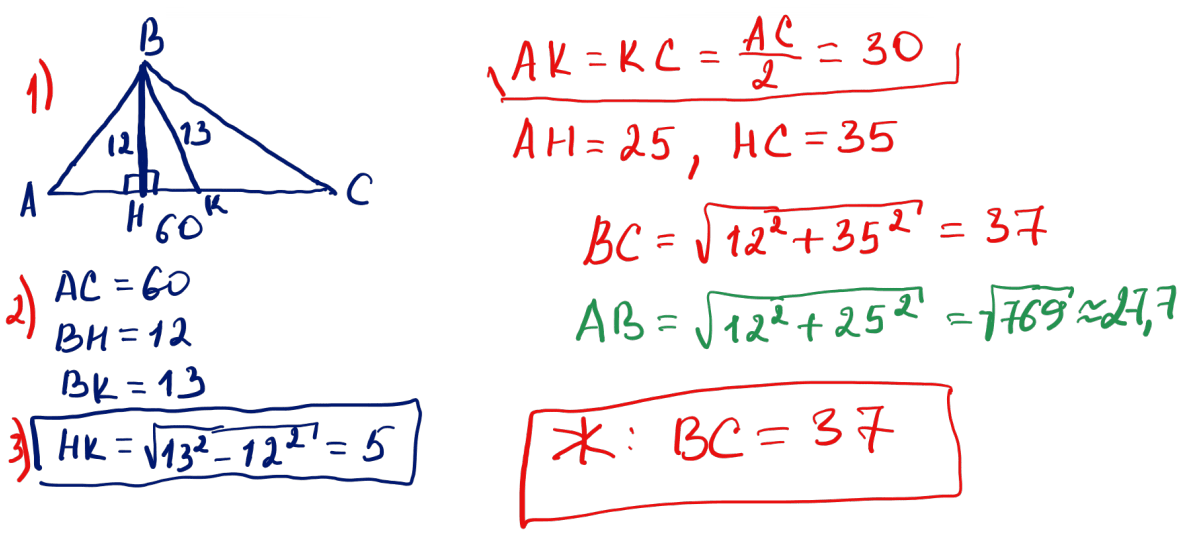
№ 3 Үшбұрыштың бұрышы $\dfrac{\pi}{3}$, ал оған қарама-қарсы қабырғасы $\sqrt{7}$-ге тең. Басқа қабырғаларының ұзындықтары $a:b=3:1$ қатынасындай. Үшбұрыштың үлкен қабырғасын табыңыз.

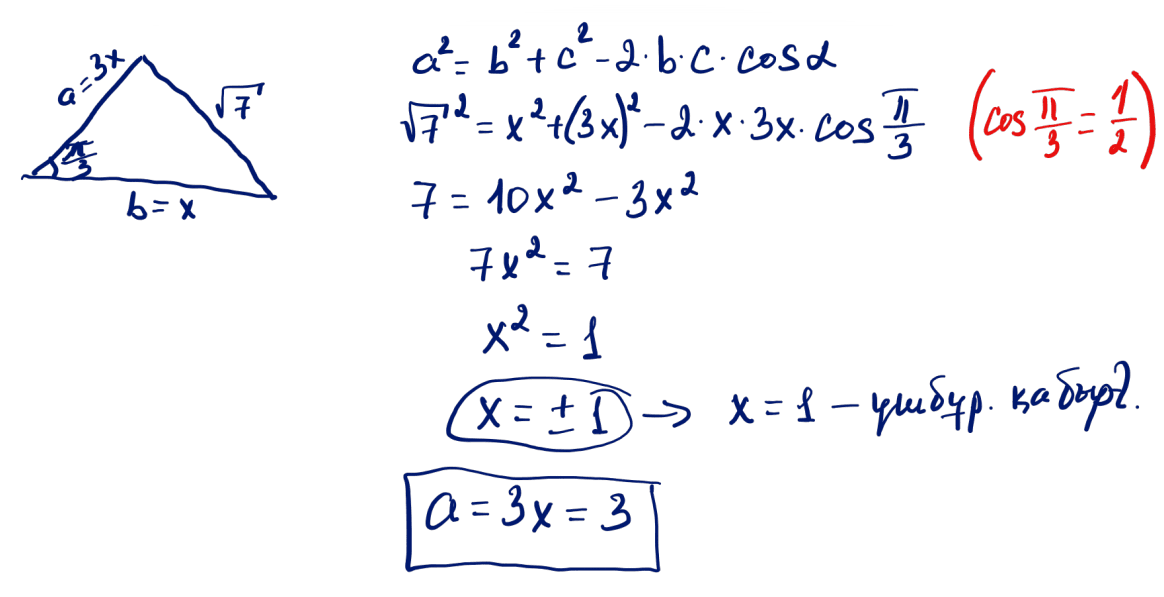
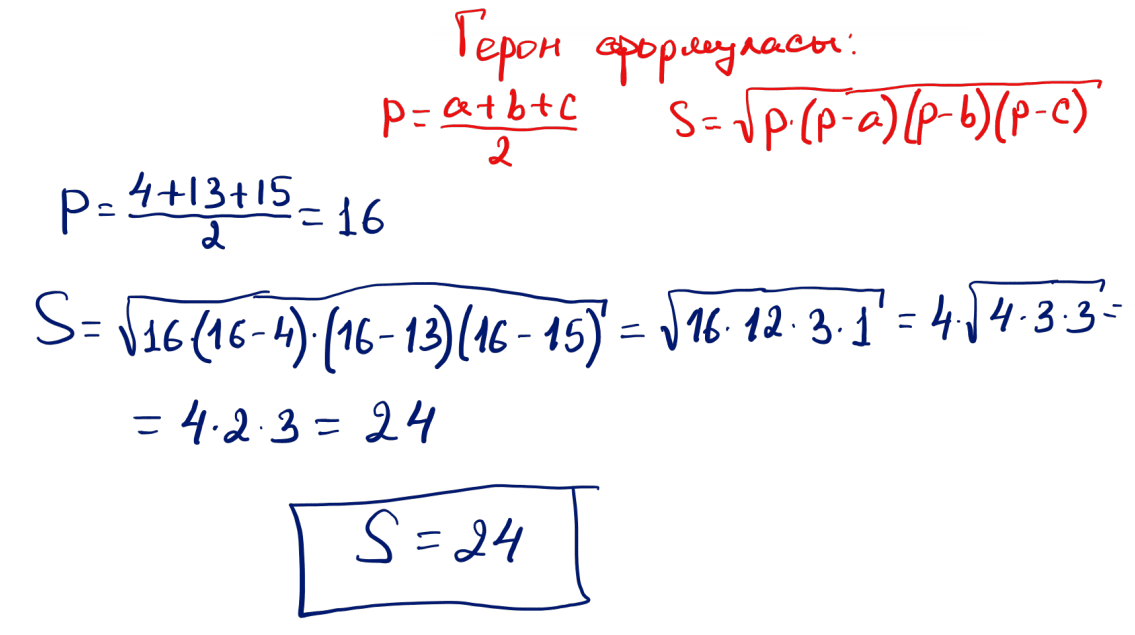
№ 4 Қабырғалары 4; 13 және 15 болатын үшбұрыштың ауданын табыңыз.

№ 5 Үшбұрышқа іштей сызылған шеңбердің радиусы 3-ке тең, ал үшбұрыштың периметрі – 20. Үшбұрыштың ауданын табыңыз.

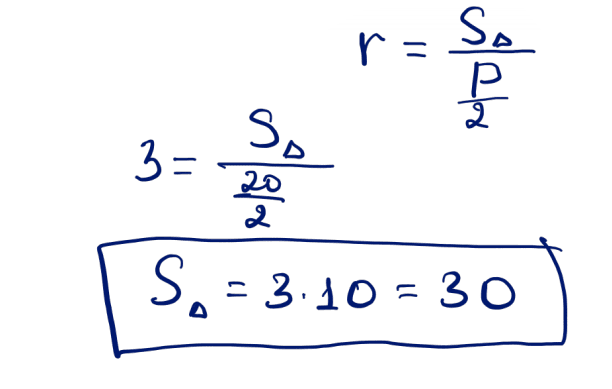
№ 6 $ABC$ үшбұрышының $AB=8$; $AC=5$; $\angle A:\angle B:\angle C=3:4:11$. Үшбұрыштың ауданын табыңыз.

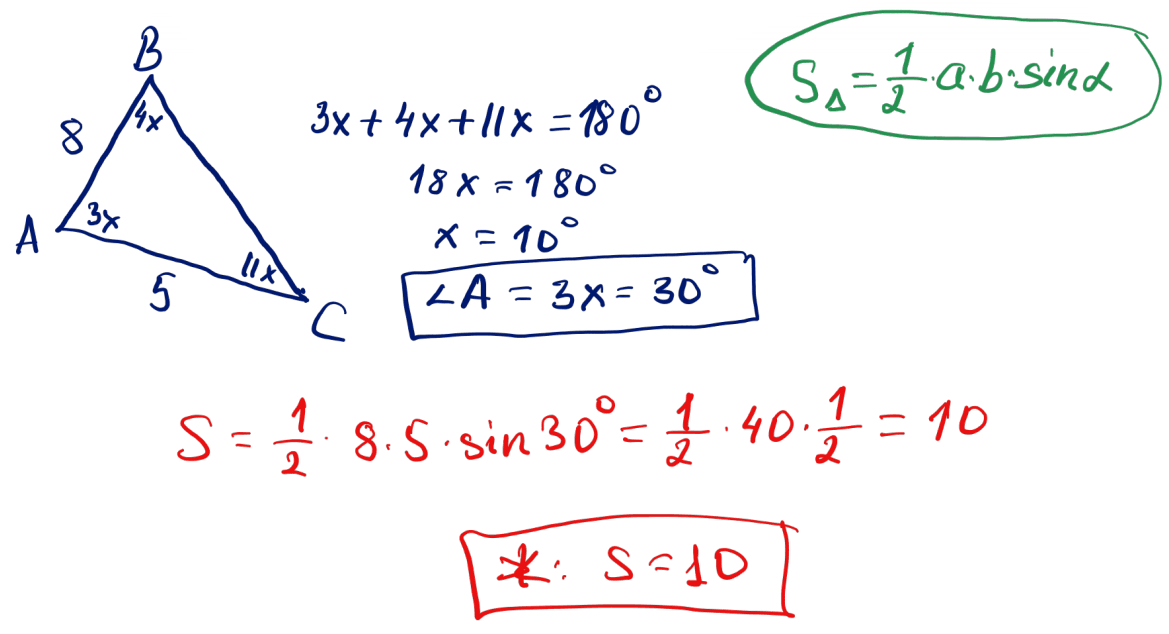
№ 7 $ABC$ үшбұрышында: $\angle A=73^\circ$, $\angle B=85^\circ$. $BC$ қабырғасына түсірілген $A$ бұрышының биссектрисасы мен биіктігінің арасындағы бұрыш қаншаға тең?

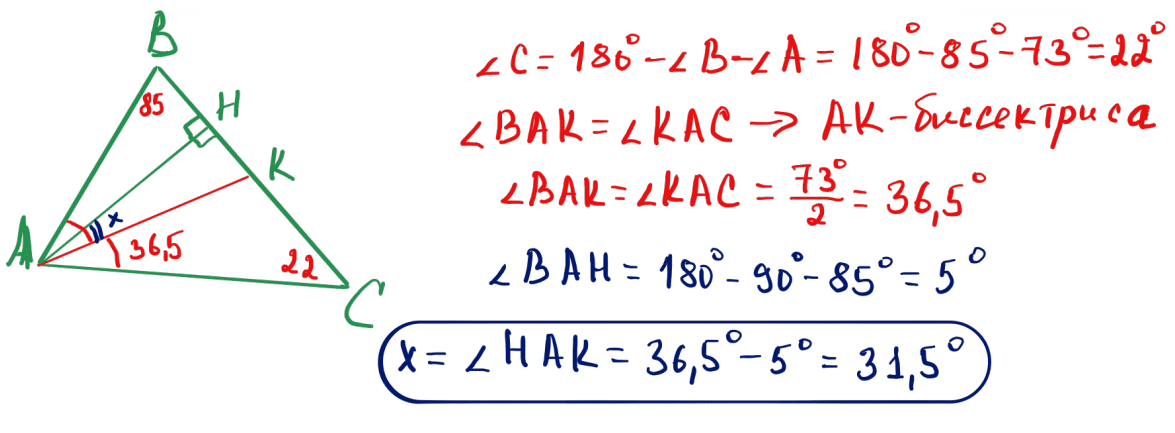
№ 8 Үшбұрыштың биіктігі 12-ге тең және 21-ге тең қабырғасын $5:16$ қатынасындай бөліктерге бөледі. Үшбұрыштың периметрін табыңыз.

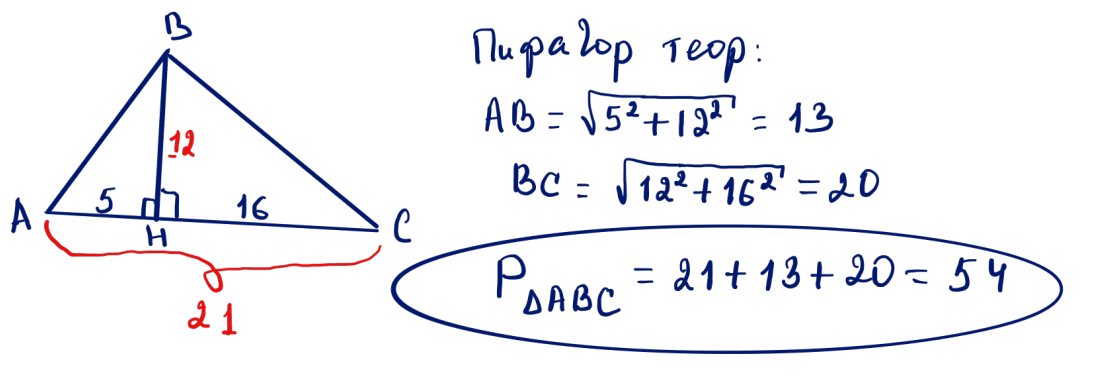
№ 9 Үшбұрыштың биіктігі 4-ке тең. Ол оны сәйкесінше периметрлері 16 және 23 болатындай екі үшбұрышқа бөледі. Осы үшбұрыштың периметрін табыңыз.

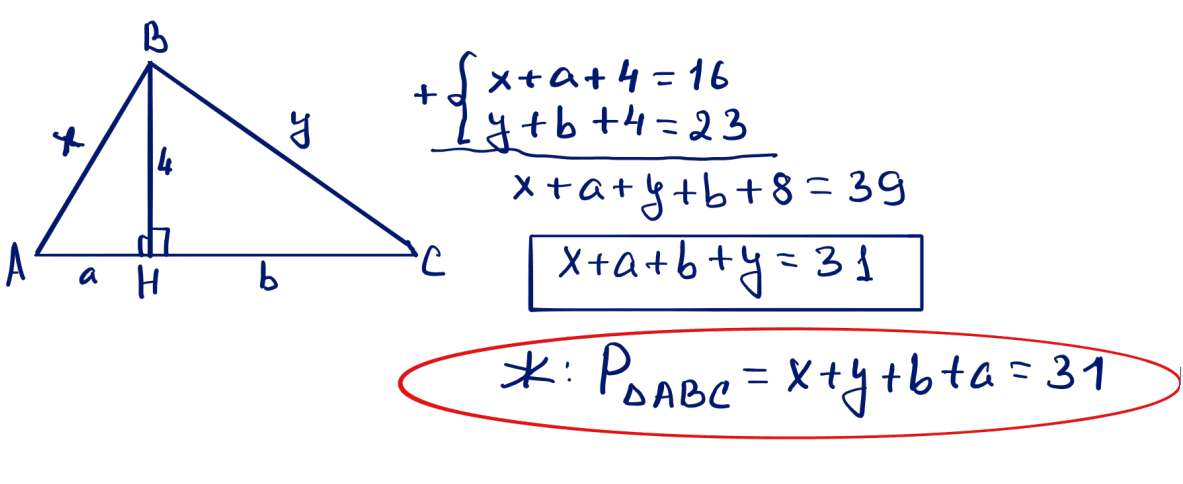
№ 10 $ABC$ үшбұрышының $AC$ қабырғасының ұзындығын табыңыз, мұндағы $B$ бұрышы доғал, $AB=13$; $BC=2$ және $\sin\angle B=\dfrac{5}{13}$

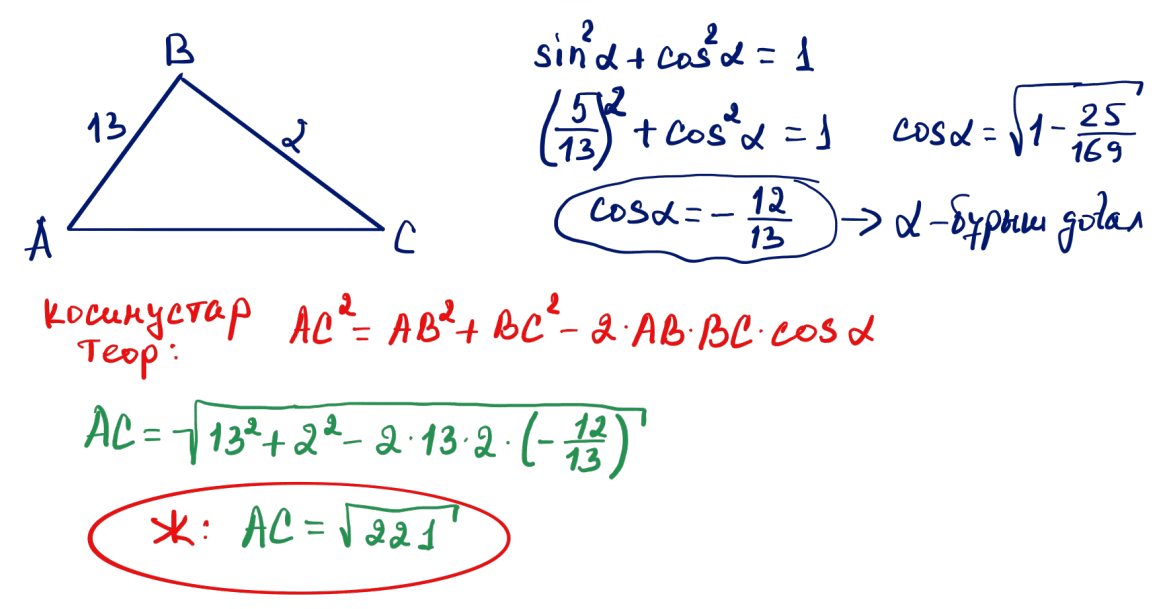
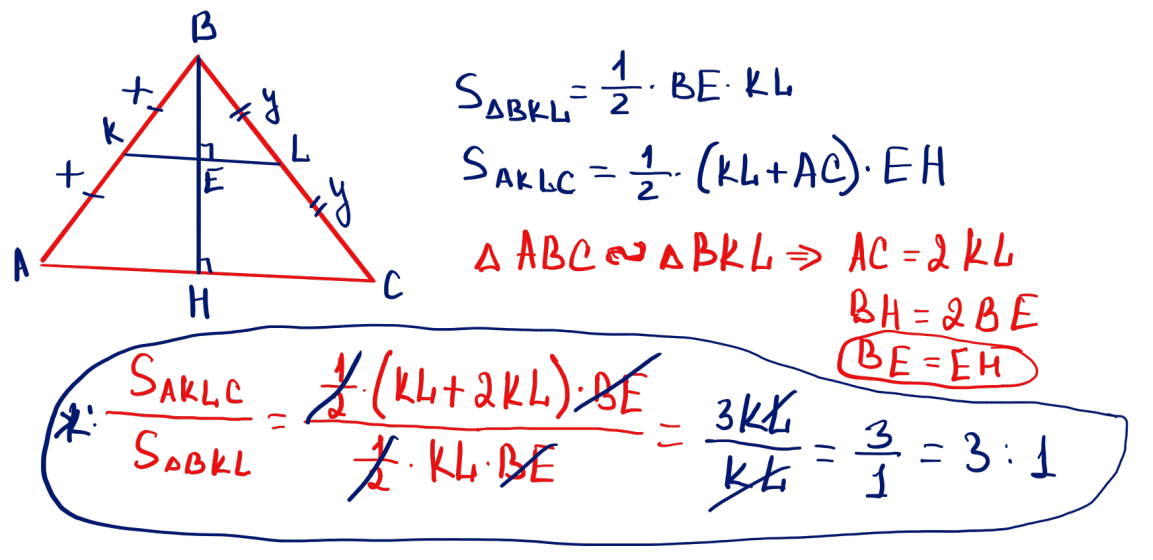
№ 11 Үшбұрышты орта сызығымен бөлгенде пайда болған төртбұрыштың ауданының үшбұрыштың ауданына қатынасын табыңыз.

№ 12 Үшбұрыштағы ұзындықтары 3 және 4 болатын екі медиана тік бұрыш жасап қиылысады. Үшбұрыштың ауданын табыңыз.

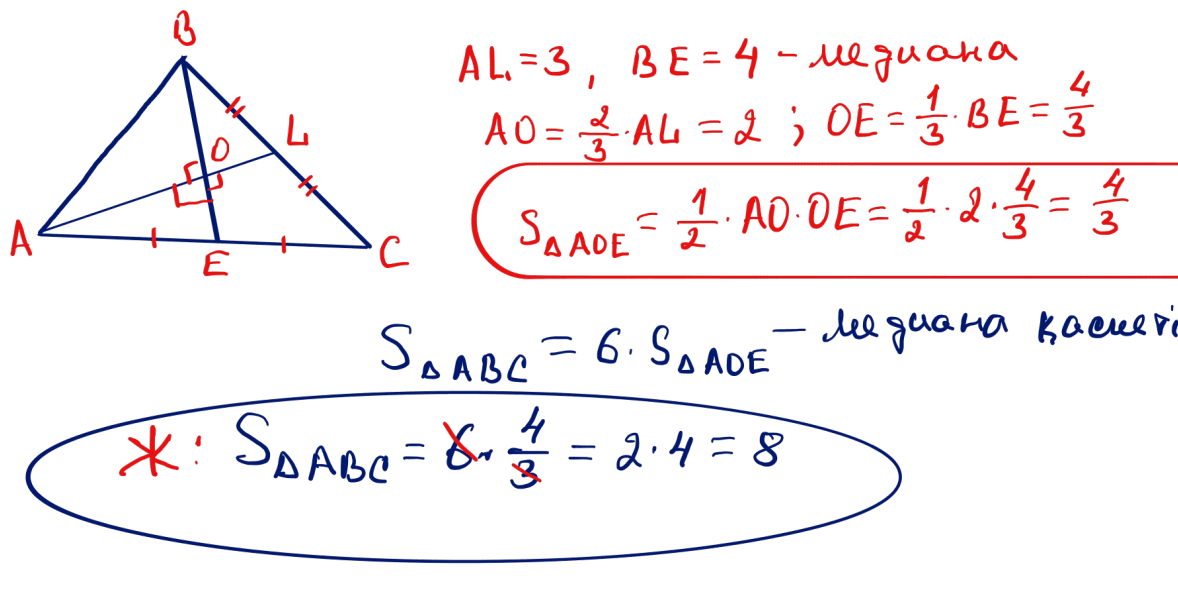
№ 13 $ABC$ үшбұрышының ауданы 36-ға тең. $AK:KC=1:5$ болатындай, $AC$ қабырғасында $K$ нүктесі алынған. $KBC$ үшбұрышының ауданын табыңыз.

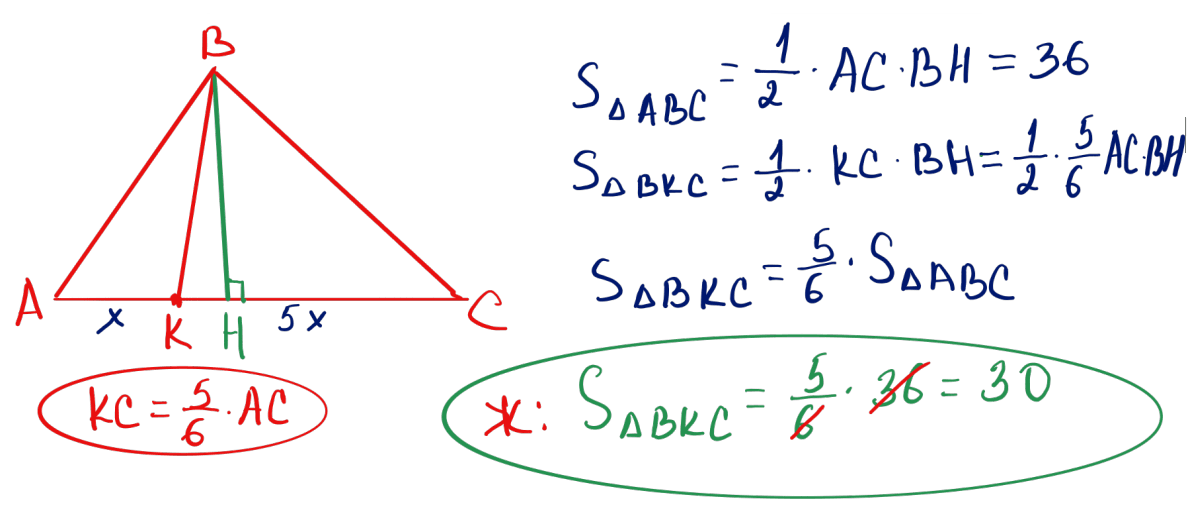
№ 14 Орта сызығы $4\sqrt{3}$, бұрыштарының шамалары 2; 3 және 4 сандарына пропорционал болатын үшбұрышқа сырттай сызылған шеңбердің радиусын есептеңіз.

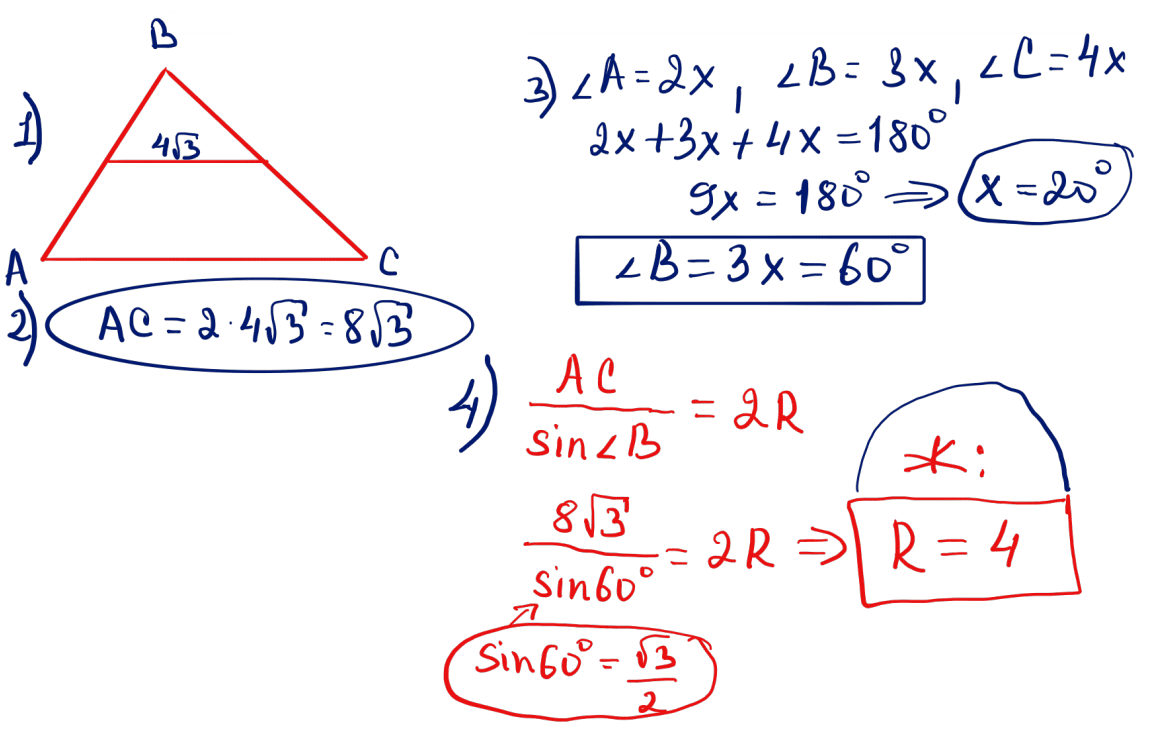
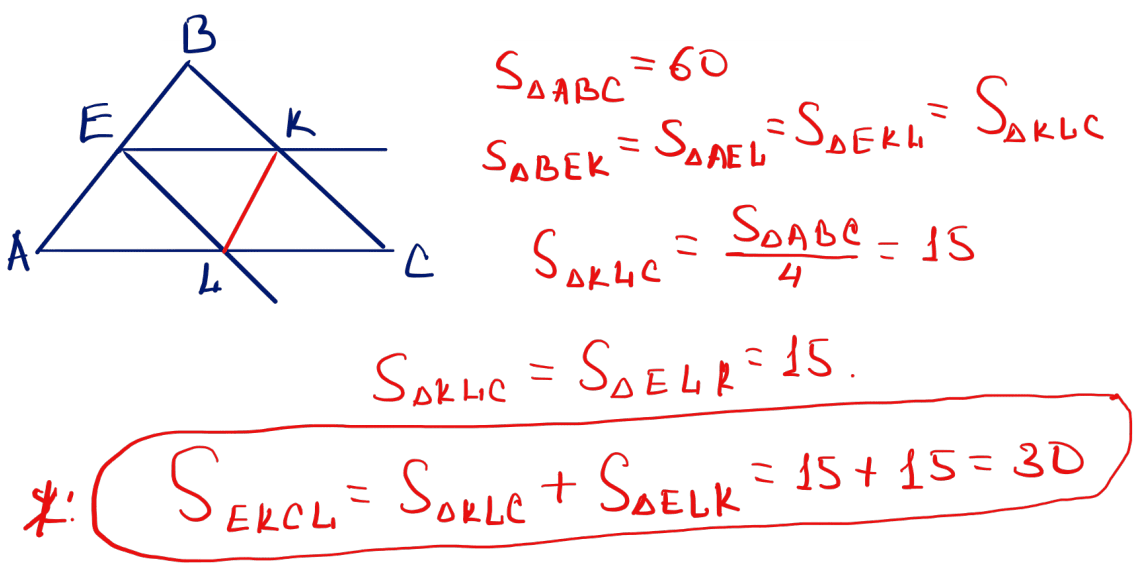
№ 15 Үшбұрыш қабырғасының ортасынан түзуелер жүргізілген, олар оның басқа екі қабырғаларына параллель. Егер осы үшбұрыштың ауданы 60 болса, шыққан төртбұрыштың ауданын табыңыз.

№ 16 $ABC$ үшбұрышында: $AB=8$; $BC=6$; $CA=3$ сәйкесінше бұрыштардың биссектрисалары $BD$ және $AE$. $ABC$ және $CDE$ үшбұрыштарының аудандарының қатынасын табыңыз.

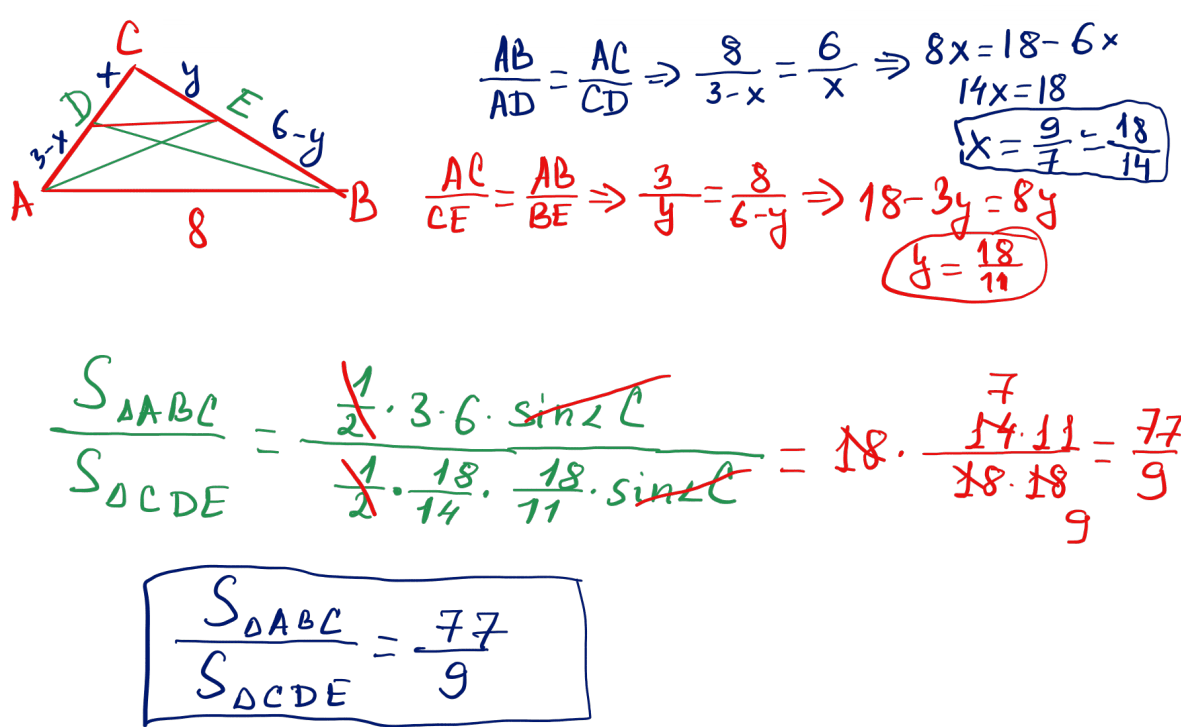
№ 17 Үшбұрыштың табаны $a$-ға тең, ал табанының бұрыштары $\dfrac{\pi}{6}$ және $\dfrac{\pi}{4}$ тең болса, үшбұрыштың ауданын табыңыз.

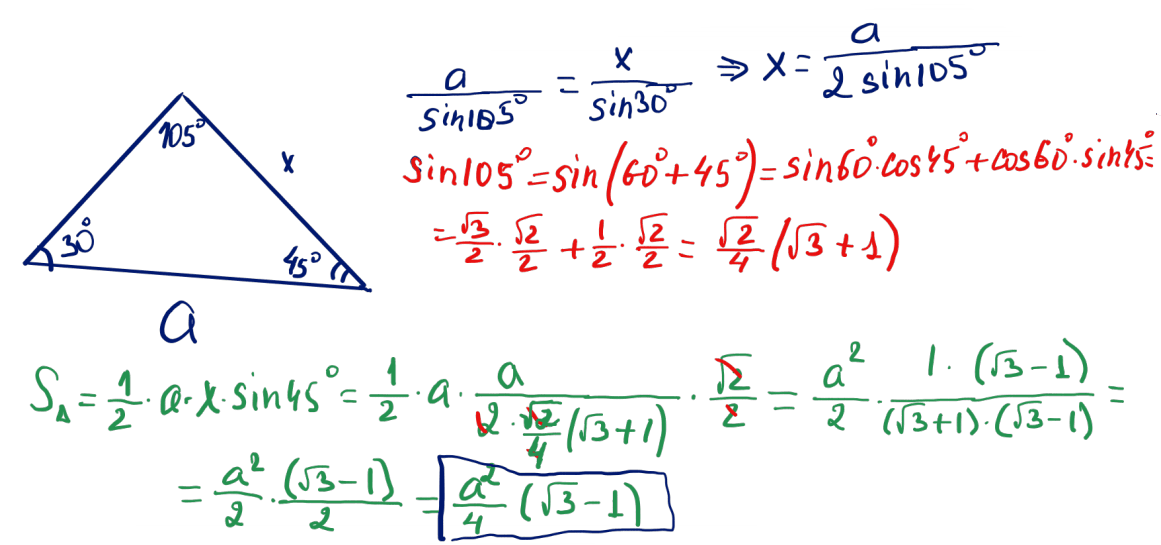
№ 18 $ABC$ үшбұрышындағы $A$ бұрышы $30^\circ$-қа тең, ал $BC$ қабырғасы $AB$ қабырғасынан екі есе артық. Егер $BDC$ үшбұрышының ауданы $4\sqrt{15}$ тең болса, $AC$ қабырғасына $B$ төбесінен жүргізілген $BD$ биіктігін табыңыз.

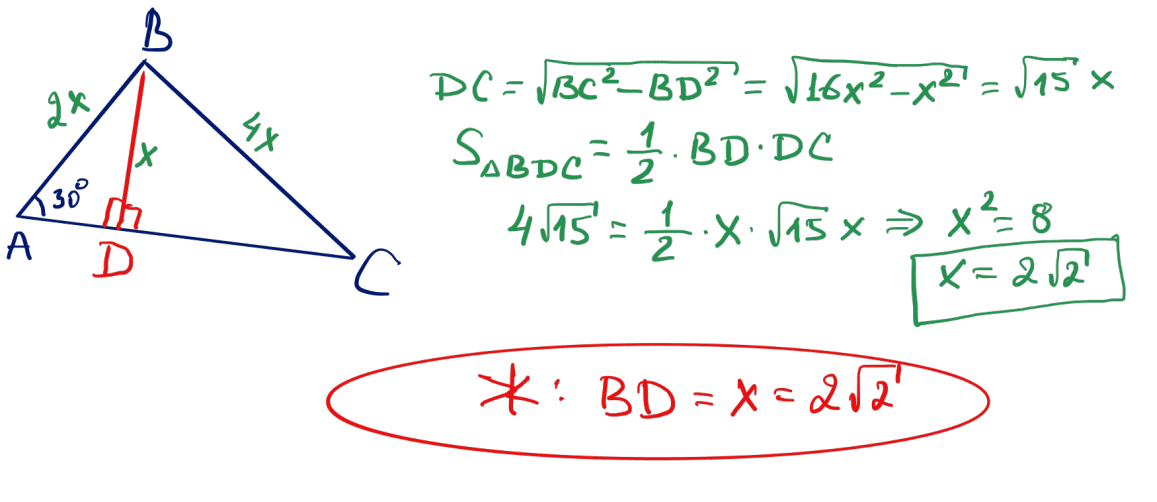
№ 19 Үшбұрыштың екі қабырғасы сәйкесінше 6 және 8. Осы қабырғаларға жүргізілген медианалар өзара перпендикуляр. Үшбұрыштың үшінші қабырғасын табыңыз.

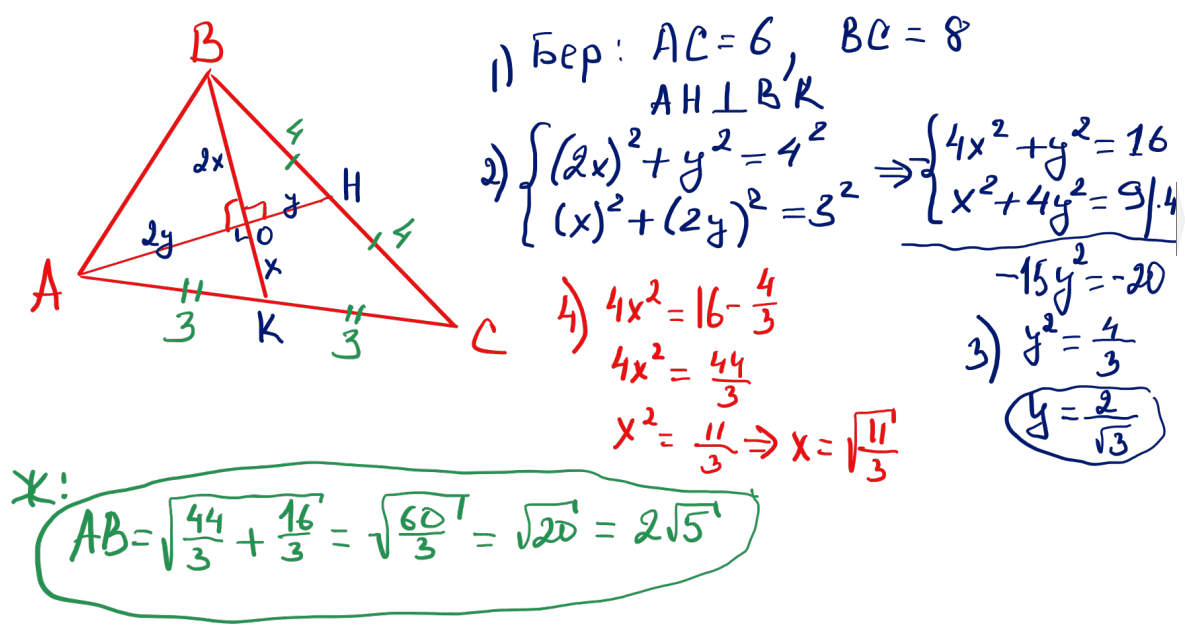
№ 20 $ABC$ үшбұрышында $\angle B=120^\circ$; $AB=7$; $AC=13$. Үшбұрыштың ауданын табыңыз.

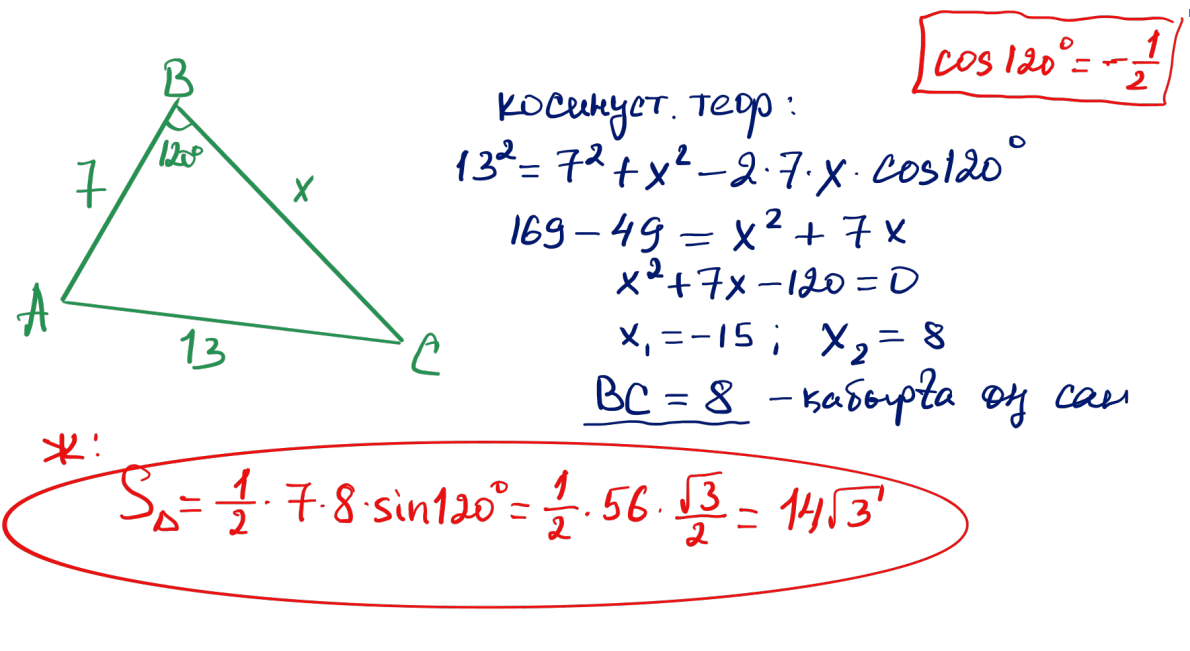
№ 21 Үшбұрыштың ішкі бұрышының биссектрисасы қабырғаны 13 және 15-ке тең кесінділерге бөледі. Екі қалған қабырғаларының қосындысы 56 болса, үшбұрыштың ауданын табыңыз.

№ 22 $MNP$ үшбұрышының $N$ бұрышының биссектрисасы $MP$ қабырғасын 28 және 12-ге тең кесінділерге бөледі. Егер $MN-NP=18$ болса, $MNP$ үшбұрышының периметрін табыңыз.

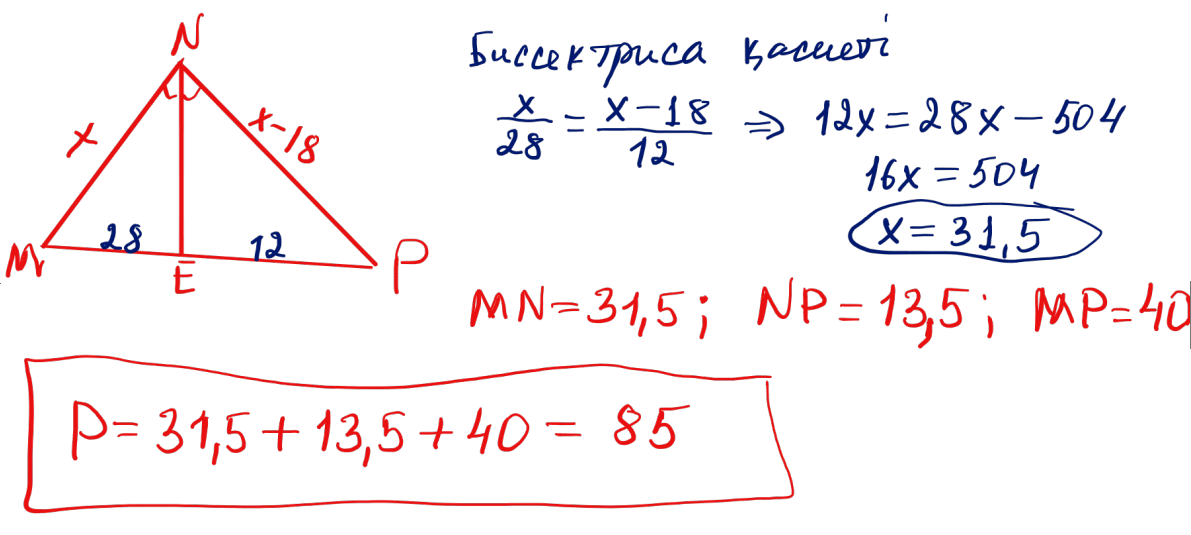
№ 23 Қабырғалары 13; 14 және 15 болатын үшбұрыштың ең кіші биіктігін табыңыз.

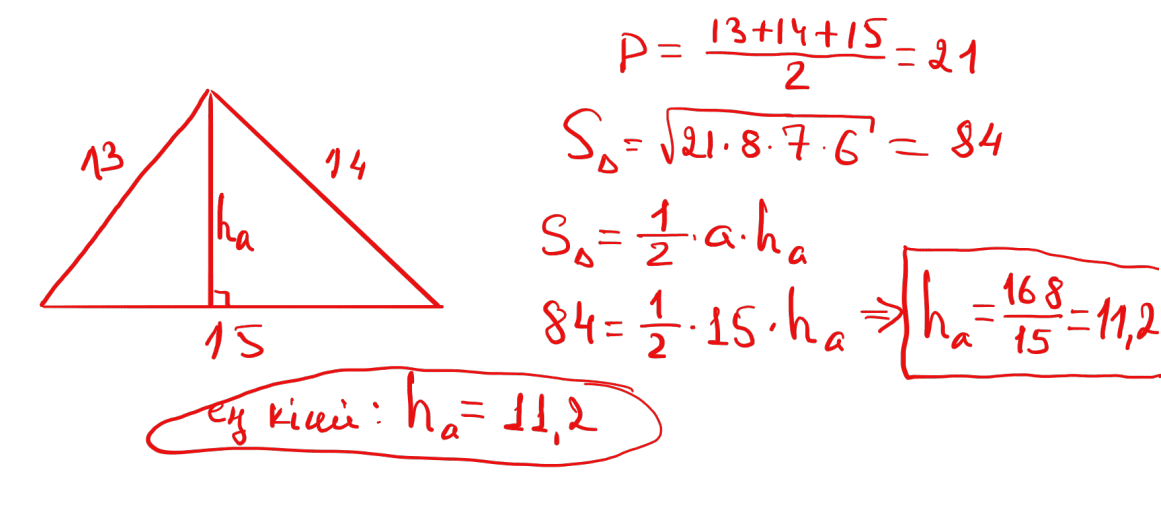
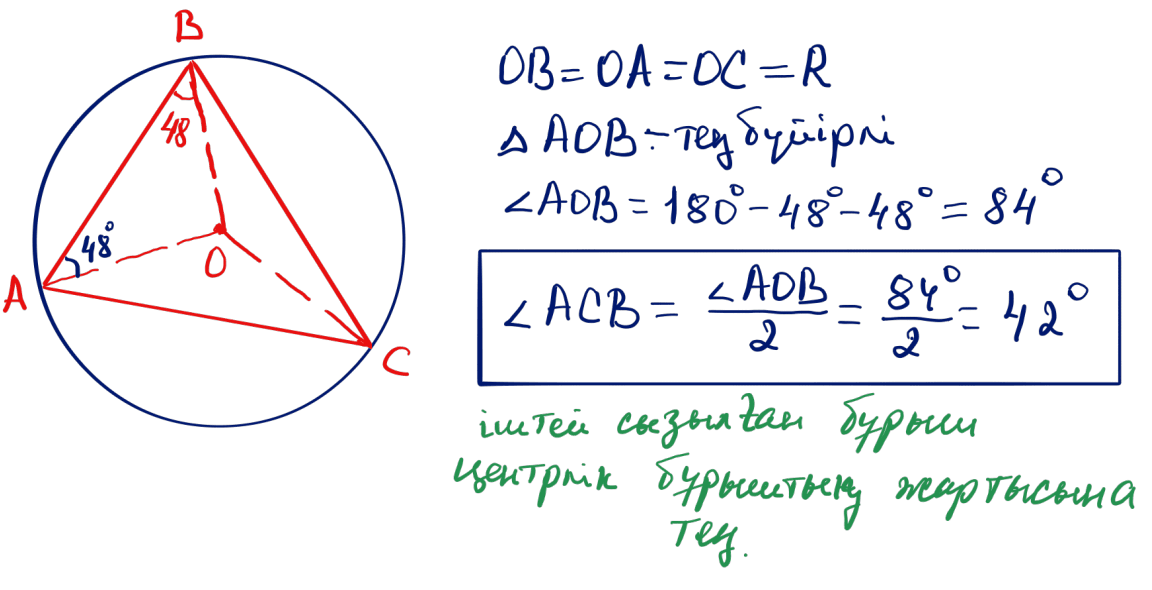
№ 24 $O$ нүктесі, $ABC$ үшбұрышының төбесінен бірдей қашықтықта, $\angle ABO=48^\circ$. $\angle ACB$ бұрышын табыңыз.

№ 25 $PQR$ үшбұрышының ауданы 36-ға тең. $S$ нүктесі $PQ$ қабырғасын $1:3$ қатынасында бөледі, ал $T$ нүктесі – $QR$ қабырғасының ортасы болып табылады. $STRP$ төртбұрышының ауданын табыңыз.

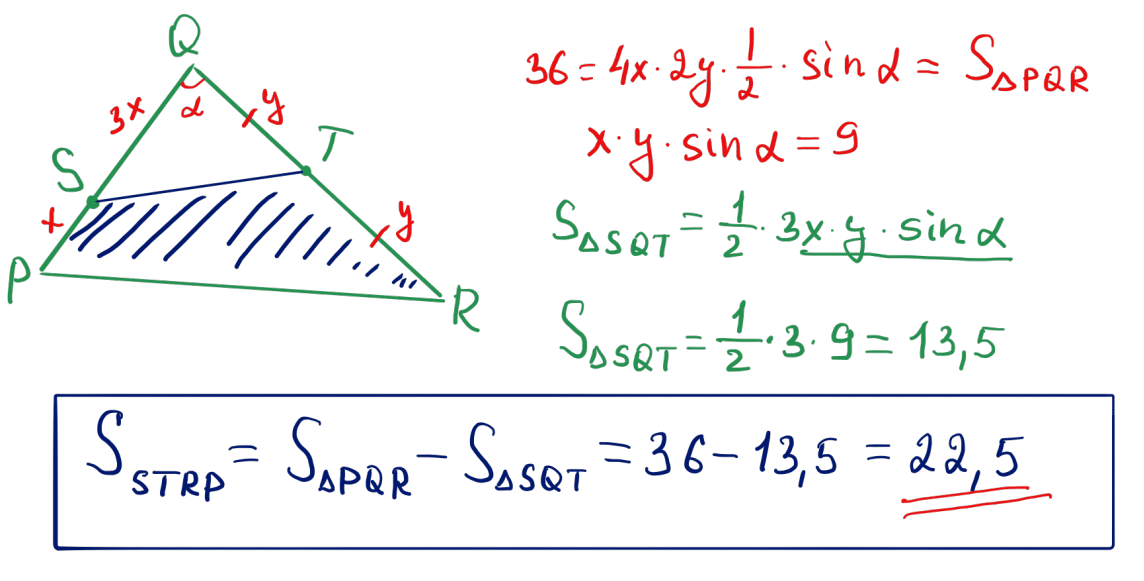
№ 26 Егер $BC=8$, ал $AC$ және $BC$-ға түсірілген биіктіктердің ұзындықтары сәйкесінше 6,4 және 4 тең болса, $ABC$ үшбұрышының $AB$ және $AC$ қабырғаларының ұзындықтарын табыңыз.

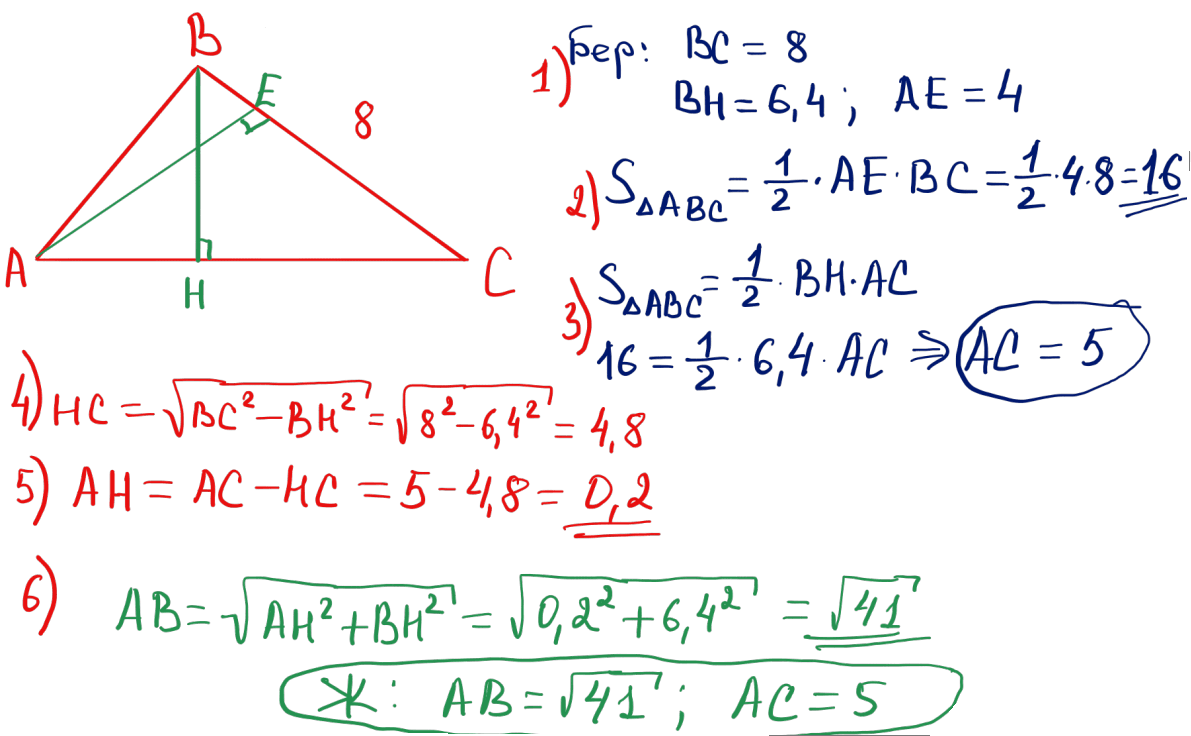
№ 27 $ABC$ үшбұрышындағы $AC$ қабырғасы 26-ға тең, ал $A$ және $C$ төбелерінен жүргізілген медианалары сәйкесінше 36 және 15. Үшінші медиананы табыңыз.

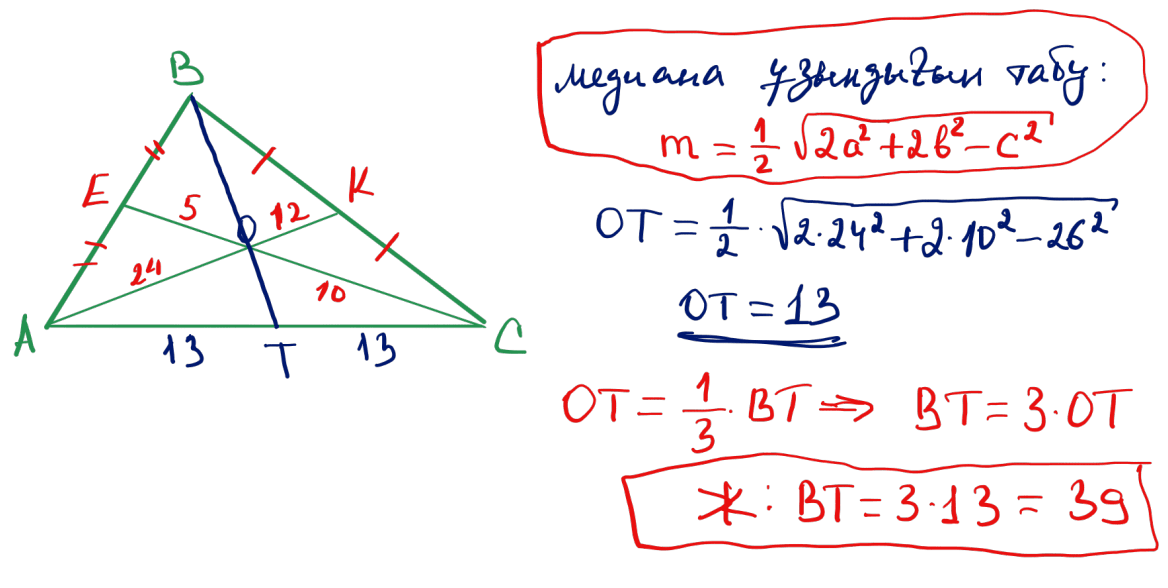
№ 28 Доғал бұрышты үшбұрыштың үлкен қабырғасы 16, ал оның екі ұшынан жүргізілген биіктіктері, доғал бұрыштың төбесінен 2 және 3-ке тең қашықтықта болады. Үшбұрыштың екі кіші қабырғаларын табыңыз.

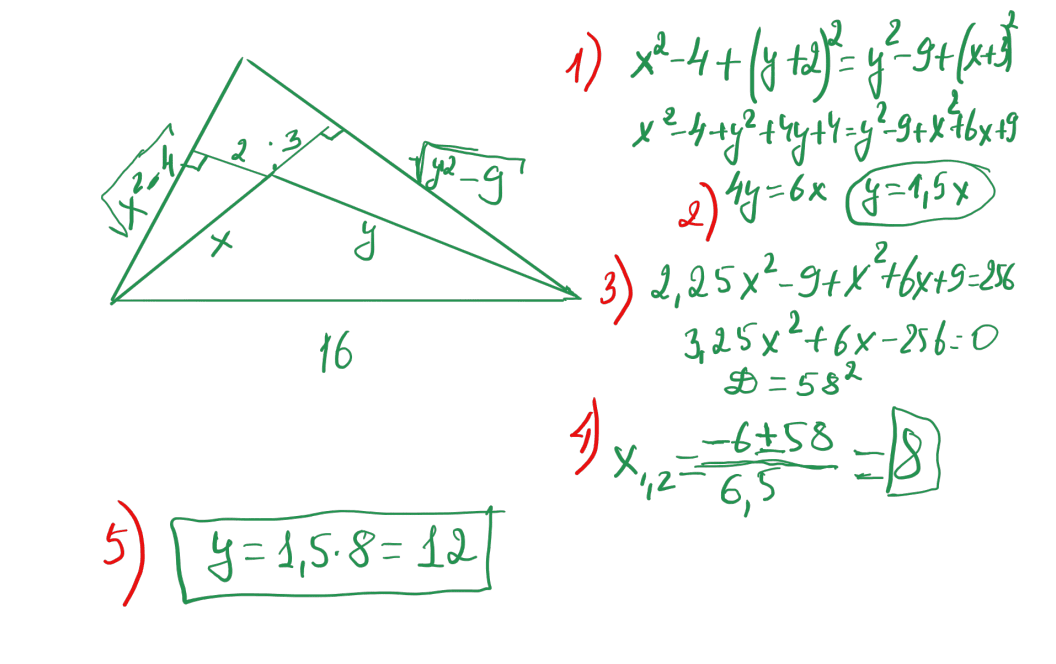
№ 29 $ABC$ үшбұрышында: $AB=6$; $BC=9$; $AC=5$; $BM$ биссектрисасы және $BN$ медианасы жүргізілген ($M\in AC$, $N\in AC$). $MN$ кесіндісінің ұзындығын табыңыз.

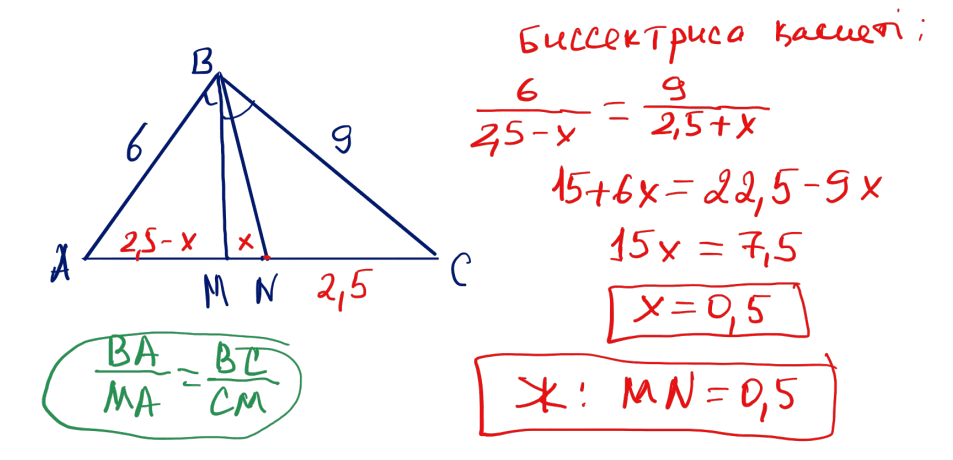
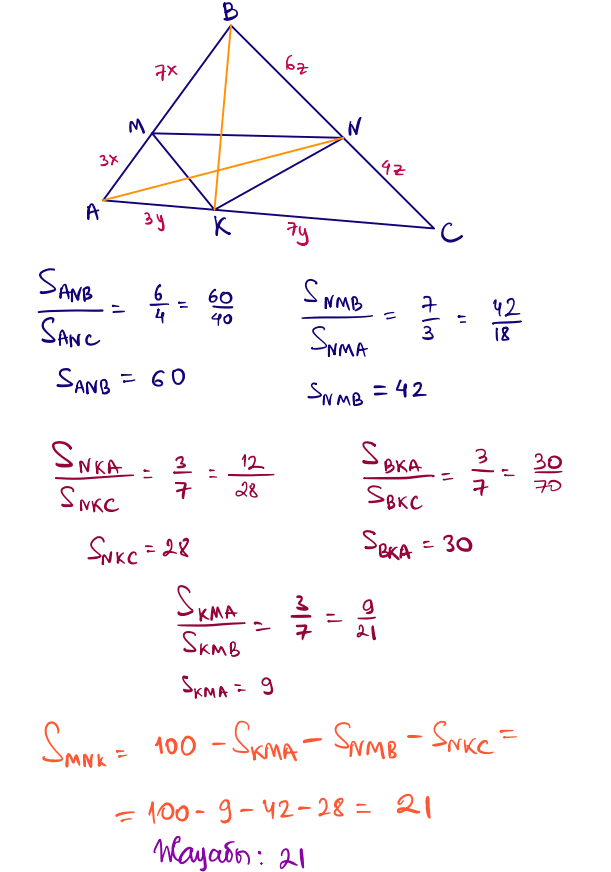
№ 30 $ABC$ үшбұрышының ауданы 100-ге тең. $M$ нүктесі $AB$ қабырғасына тиісті, мұндағы $AM:AB=3:10$. $N$ нүктесі $BC$ қабырғасына тиісті, мұндағы $BN:BC=6:10$. $K$ нүктесі $CA$ қабырғасына тиісті, мұндағы $CK:CA=7:10$. $MNK$ үшбұрышының ауданын табыңыз.

№ 31 Үшбұрышқа (қабырғалары 6; 9; 11) іштей дөңгелек салынған. Үшбұрыштың қабырғалары жанасу нүктелерімен бөлінген. Барлық алты бөліктің ішінен кішісінің ұзындығын табыңыз.

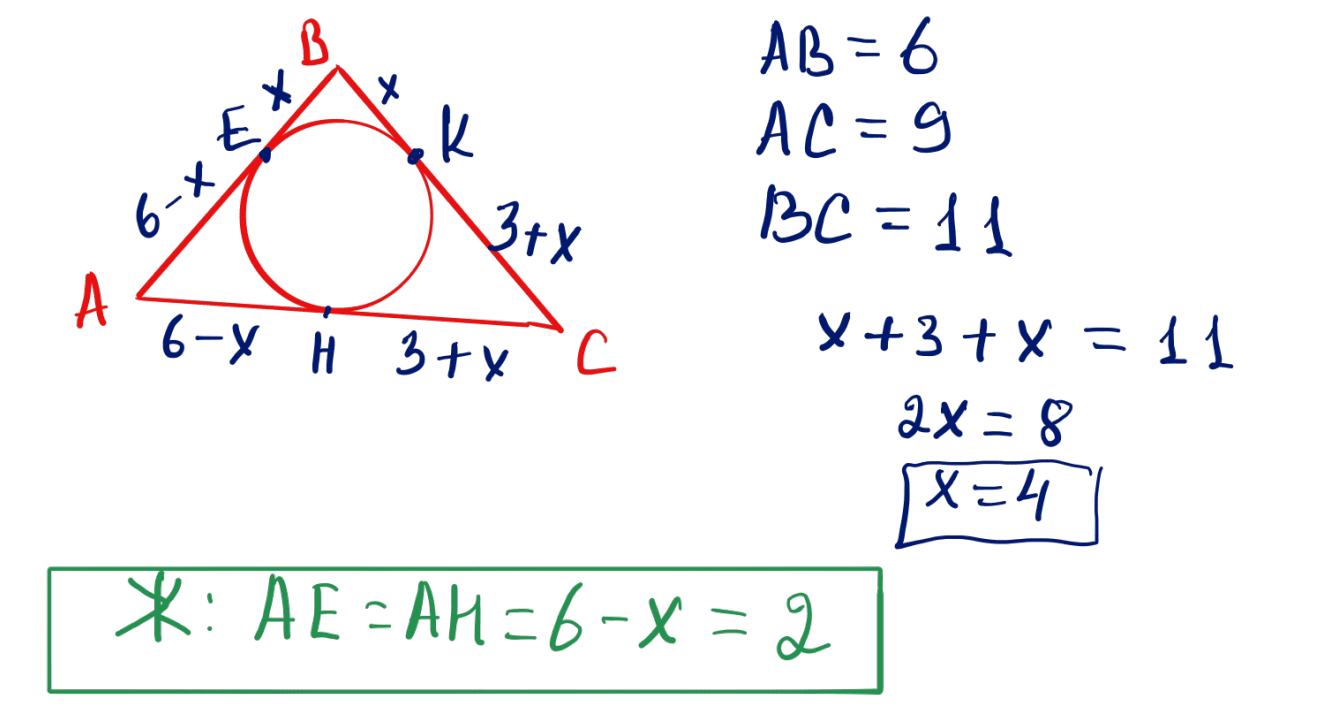
№ 32 $ABC$ үшбұрышында $AB=19$, бұрыштары $\angle A=\arctan\dfrac{5}{2}$, $\angle B=\arctan\dfrac{2}{3}$. $ABC$ үшбұрышының ауданын табыңыз.

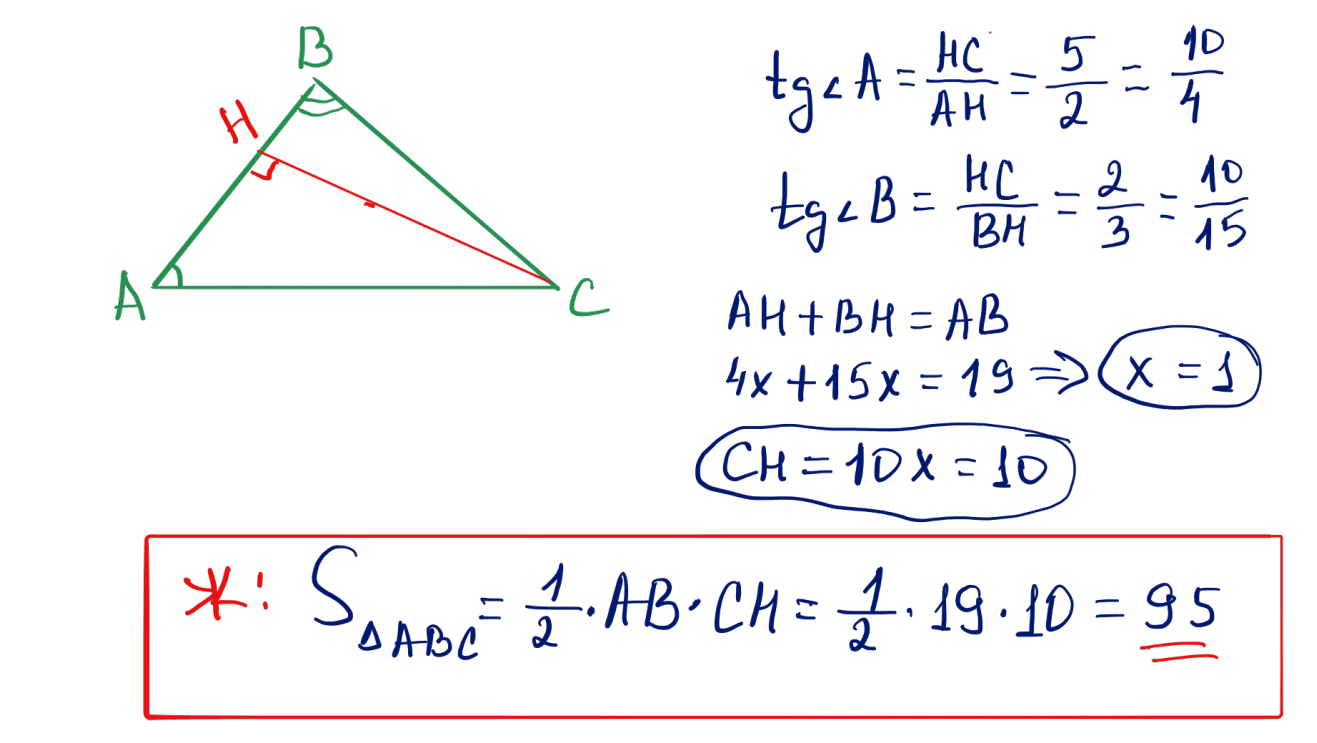
№ 33 $ABC$ үшбұрышында $BM$ биссектрисасы және $BN$ биіктігі жүргізілген, мұндағы $M\in AC$ және $N\in AC$; $AM=8$; $MN=1$; $NC=3$. $BN$ биіктігінің квадратын табыңыз.

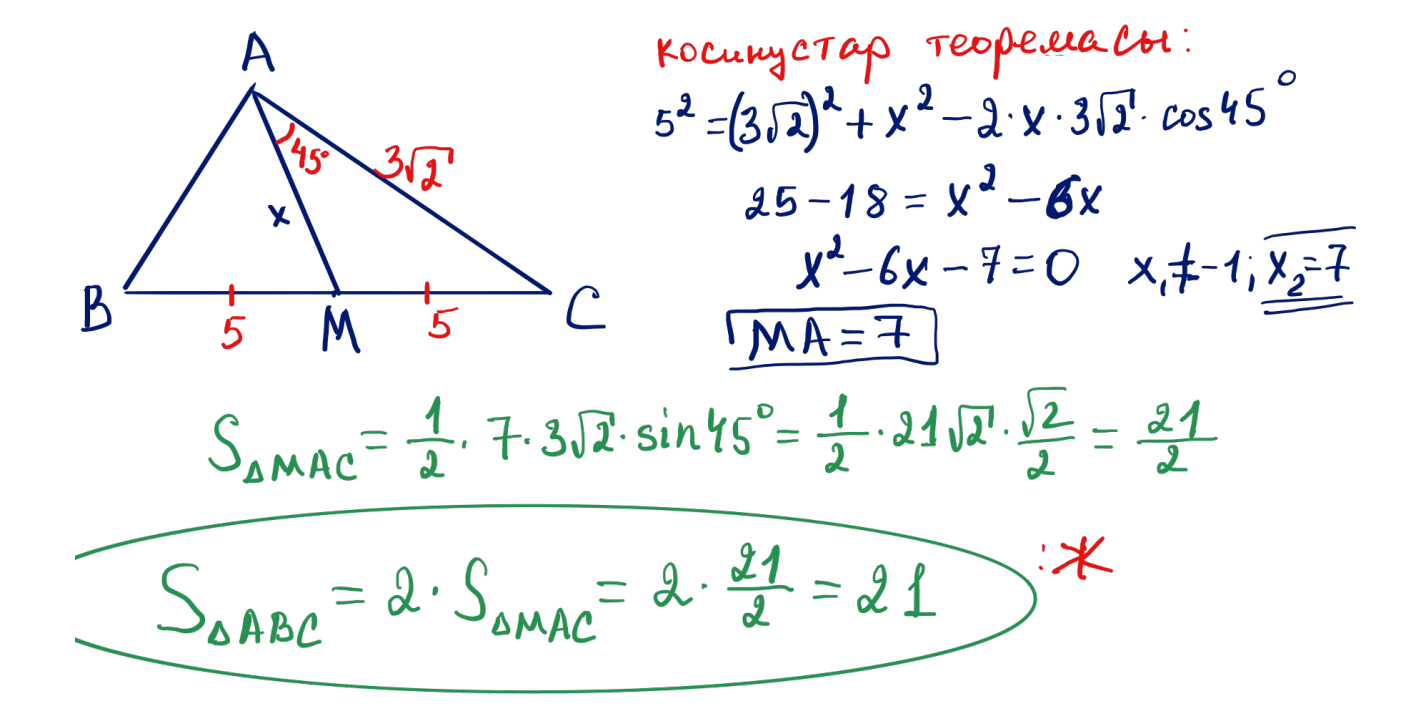
№ 34 $ABC$ үшбұрышында $AM$ медианасы жүргізілген. Егер $AC=3\sqrt{2}$, $BC=10$, $\angle MAC=45^\circ$ болса, $ABC$ үшбұрышының ауданын табыңыз.

№ 35 $BK=12$, $AK=4$, $\angle BOK=\angle BAO$, $\cos\angle B=\dfrac{\sqrt{6}}{3}$ болатындай $ABO$ үшбұрышының $AB$ қабырғасында $K$ нүктесі жатыр. $OBK$ үшбұрышының ауданын табыңыз.

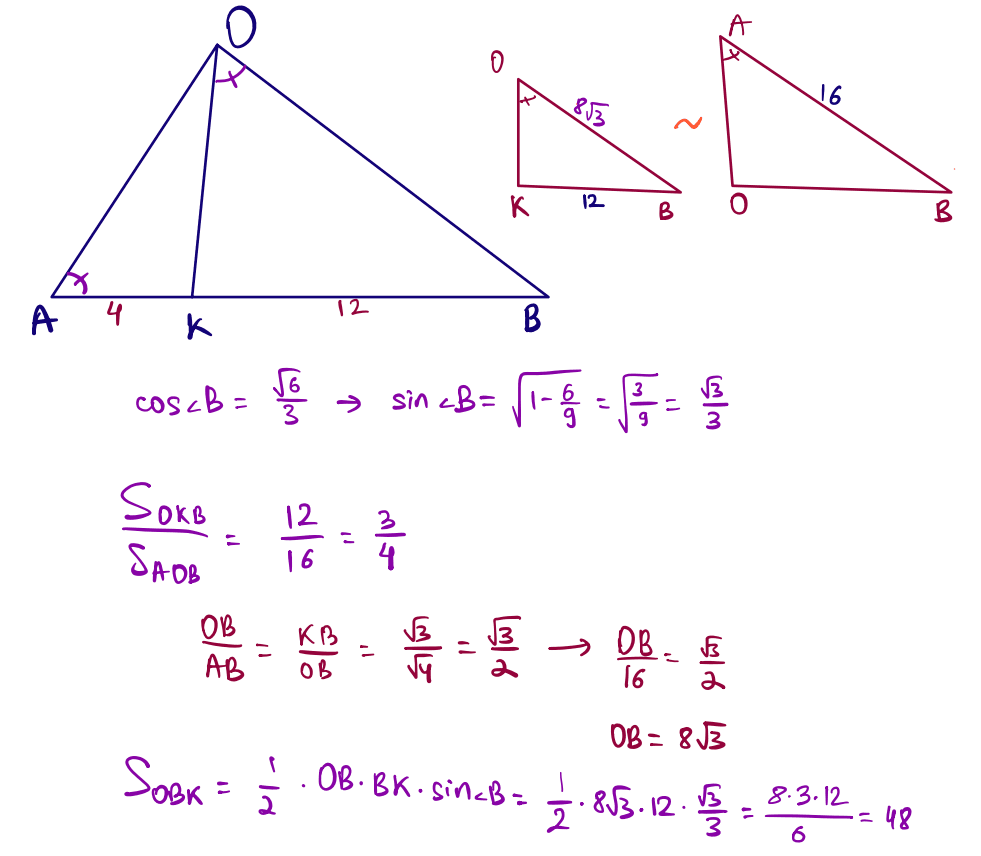
№ 36 $\angle C=30^\circ$, $AB=5$, $BC=8$ болатындай $ABC$ үшбұрышында $A$ бұрышы – доғал. $AC$ қабырғасын табыңыз.

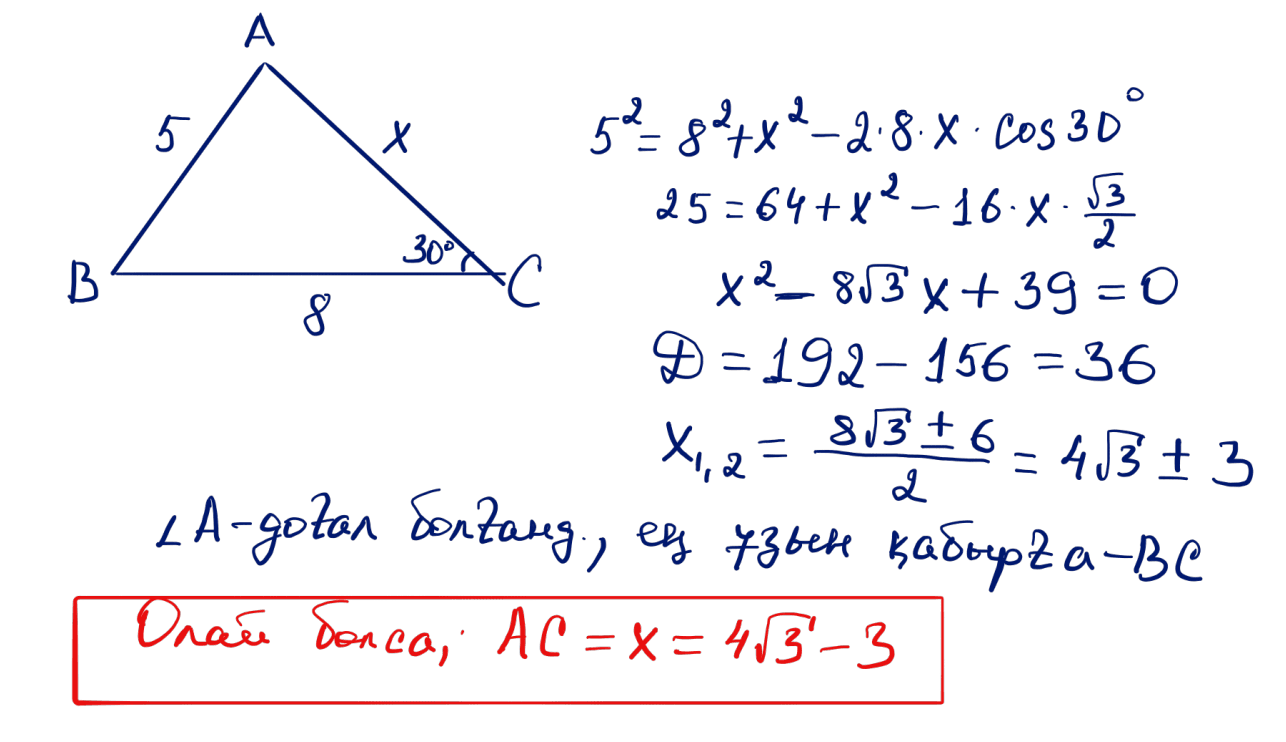
№ 37 $ABC$ үшбұрышының $BC$ қабырғасы 25-ке тең, биіктігі $BD=15$, оған сырттай сызылған шеңбердің радиусы $R=32{,}5$. Үшбұрыштың қалған екі қабырғаларын анықтаңыз.

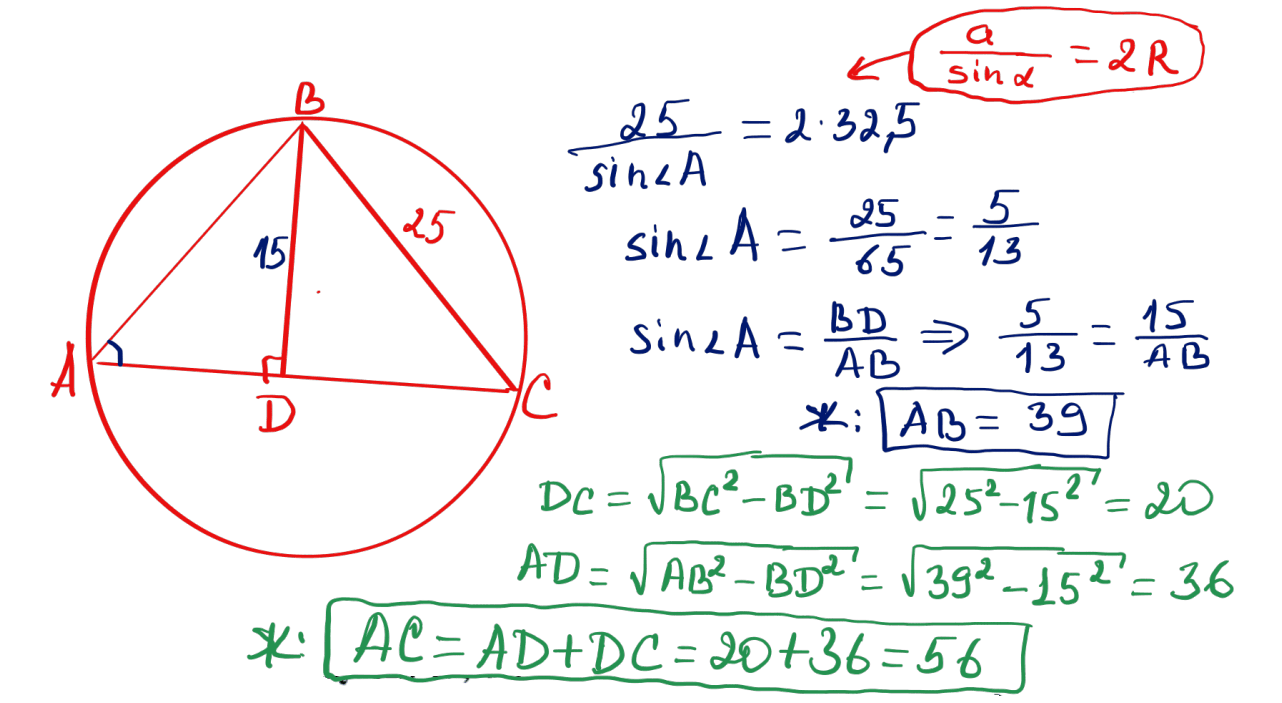
№ 38 Үшбұрыштың екі сүйір бұрышының синустары $\dfrac{3}{5}$ және $\dfrac{5}{13}$-ке тең, ал оған сырттай сызылған шеңбердің радиусы 32,5. Үшбұрыштың ауданын табыңыз.

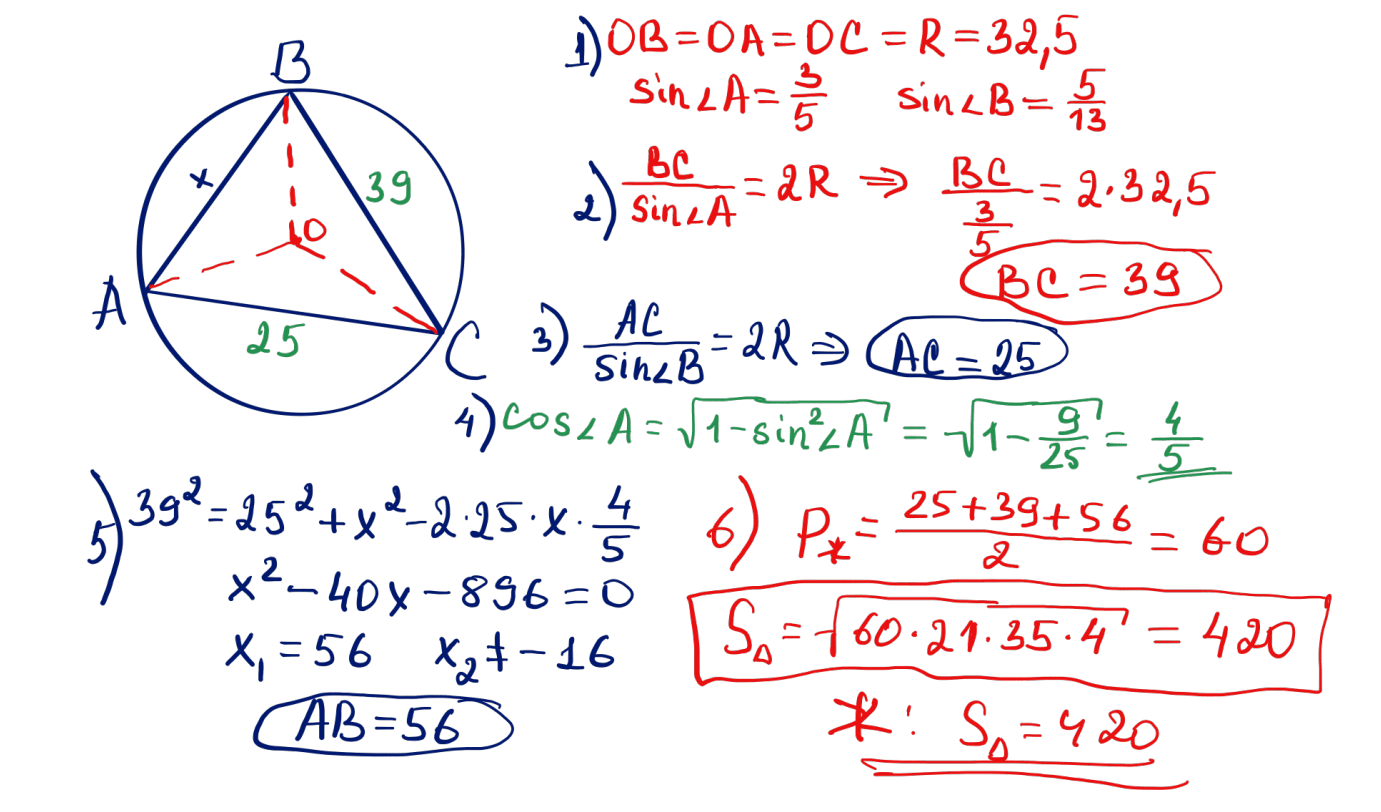
№ 39 Үшбұрыштың екі қабырғасы 2 және $2\sqrt{15}$, ал үшінші қабырғасының медианасы 4. Үшбұрыштың ауданын табыңыз.

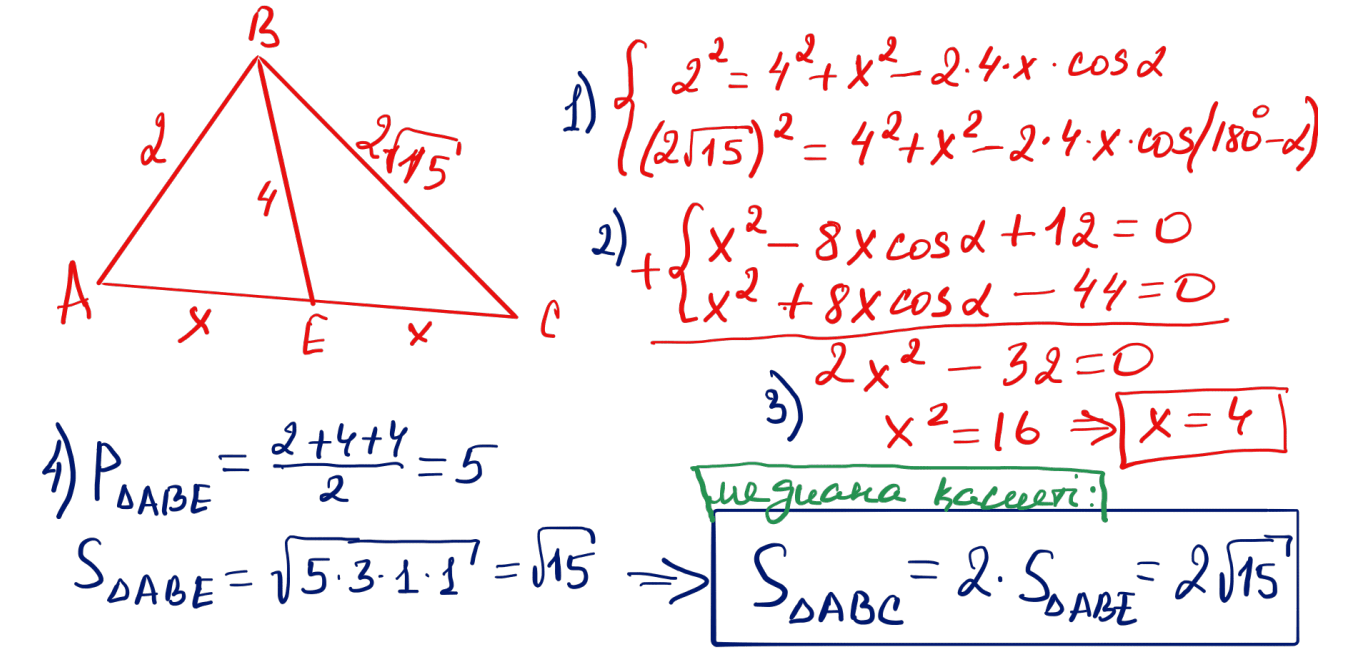
№ 40 $MNK$ үшбұрышында $\angle MNK$ бұрышы – доғал. $MD$ және $KE$ биіктіктері $P$ нүктесінде қиылысады. $PN=5$; $MK=10$. $MNKP$ төртбұрышының ауданын табыңыз.