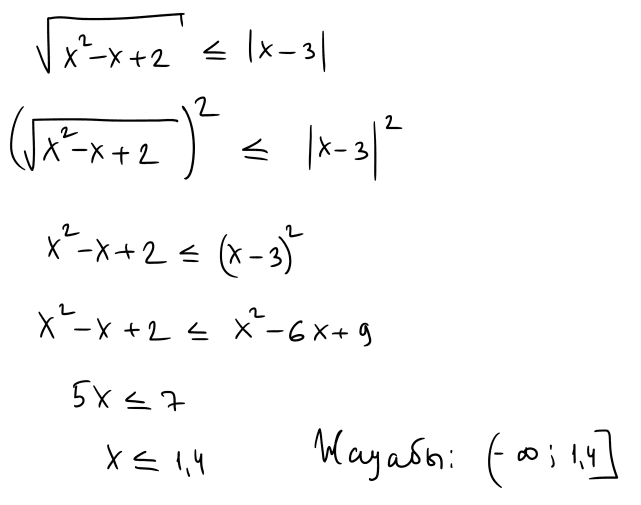1.7.6. Теңсіздіктерді шешу (жоғары деңгей)

Жауаптарын көрсету/жасыру

№ 1 Теңсіздікті шешіңіз: $4|x-5|-x^2+10 x-20\gt 0$

№ 2 Теңсіздікті шешіңіз: $\dfrac{x^2-7|x|+10}{x^2-6 x+9}\lt 0$

№ 3 Теңсіздікті шешіңіз: $\dfrac{\left|x^2-4 x\right|+3}{x^2+|x-5|} \geq 1$

№ 4 Теңсіздікті шешіңіз: $|5-x|\lt |2-x|+|2 x-7|$

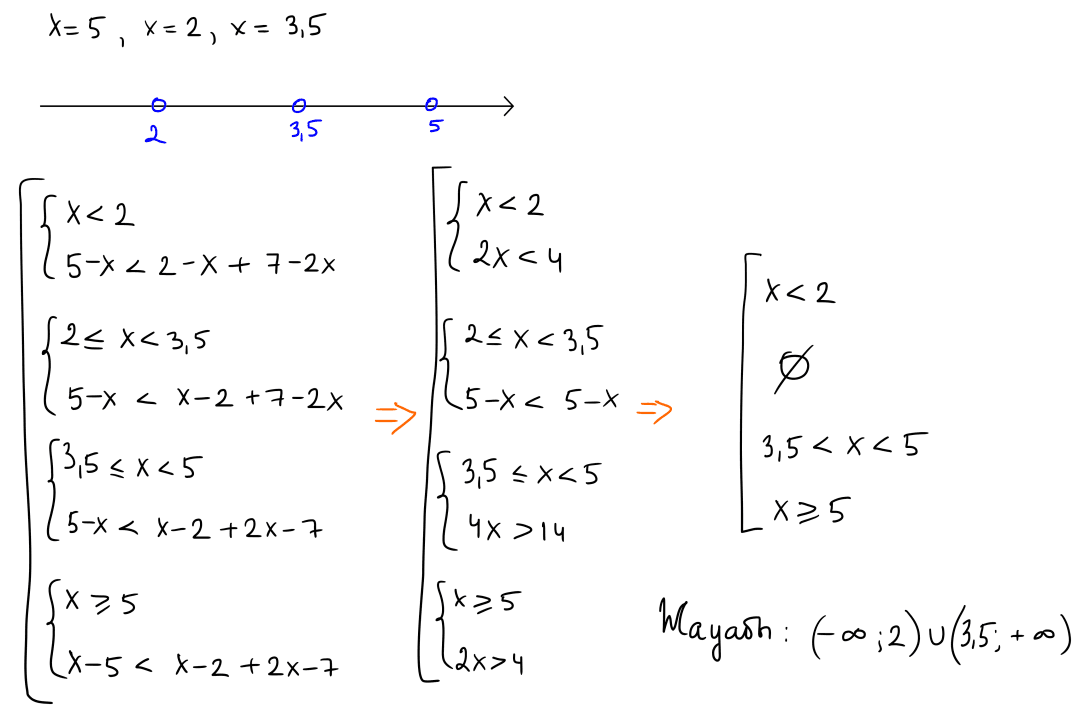
№ 5 Теңсіздікті шешіңіз: $||2 x^2-x|-3| \leq 2 x^2+x+5$

№ 6 Теңсіздікті шешіңіз: $\left|\dfrac{x^2-5 x+4}{x^2-4}\right| \leq 1$

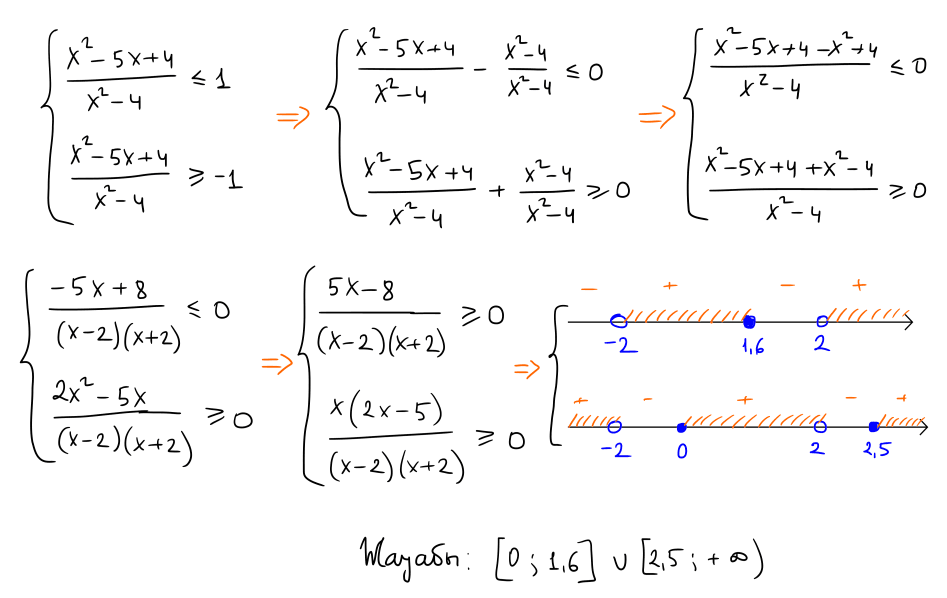
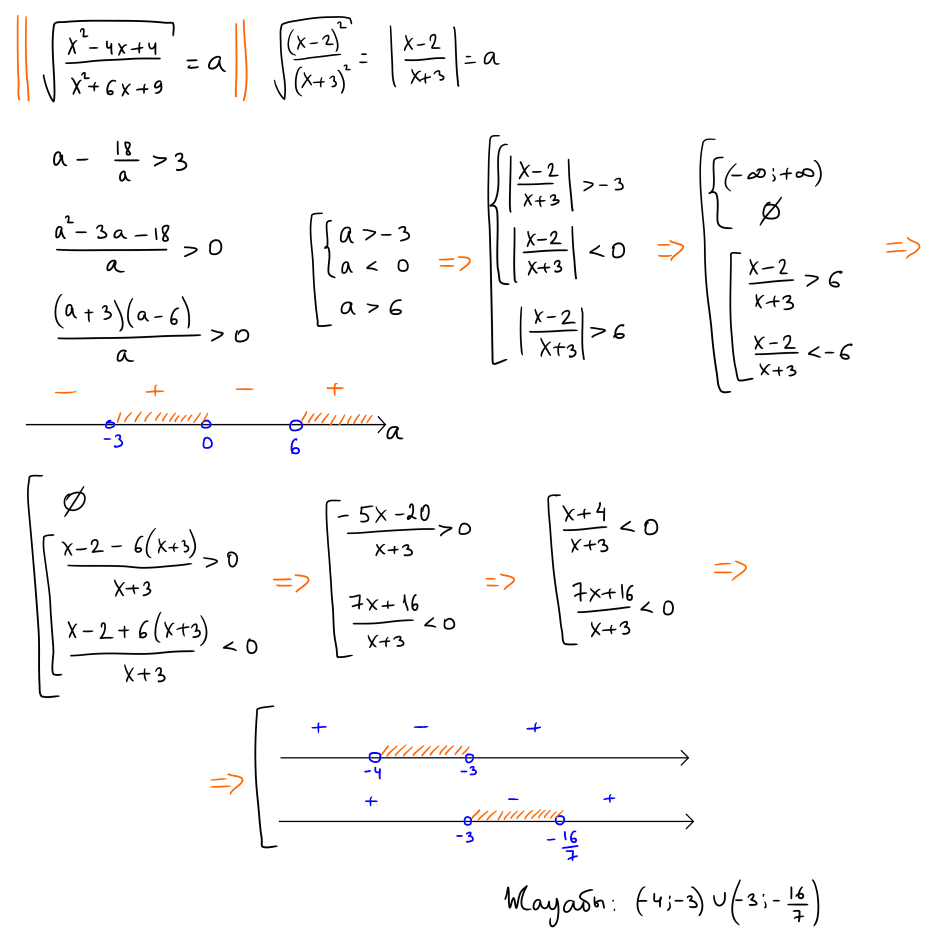
№ 7 Теңсіздікті шешіңіз: $\sqrt{\dfrac{x^2-4 x+4}{x^2+6 x+9}}-18 \sqrt{\dfrac{x^2+6 x+9}{x^2-4 x+4}}\gt 3$

№ 8 Теңсіздікті шешіңіз: $\dfrac{x^2+2|x|-2}{x+1} \leq 3 x$

№ 9 Теңсіздікті шешіңіз: $\left\{\begin{array}{l}\dfrac{28-x^2}{9}-\dfrac{x}{3} \geq 0 \\ |x+7| \cdot(3 x+7) \geq 0\end{array}\right.$

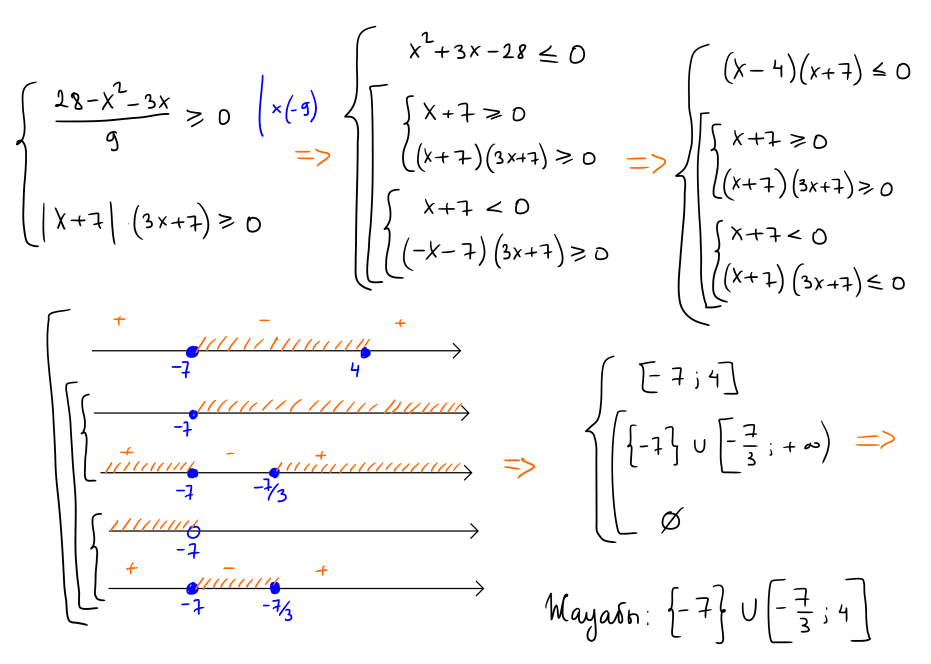
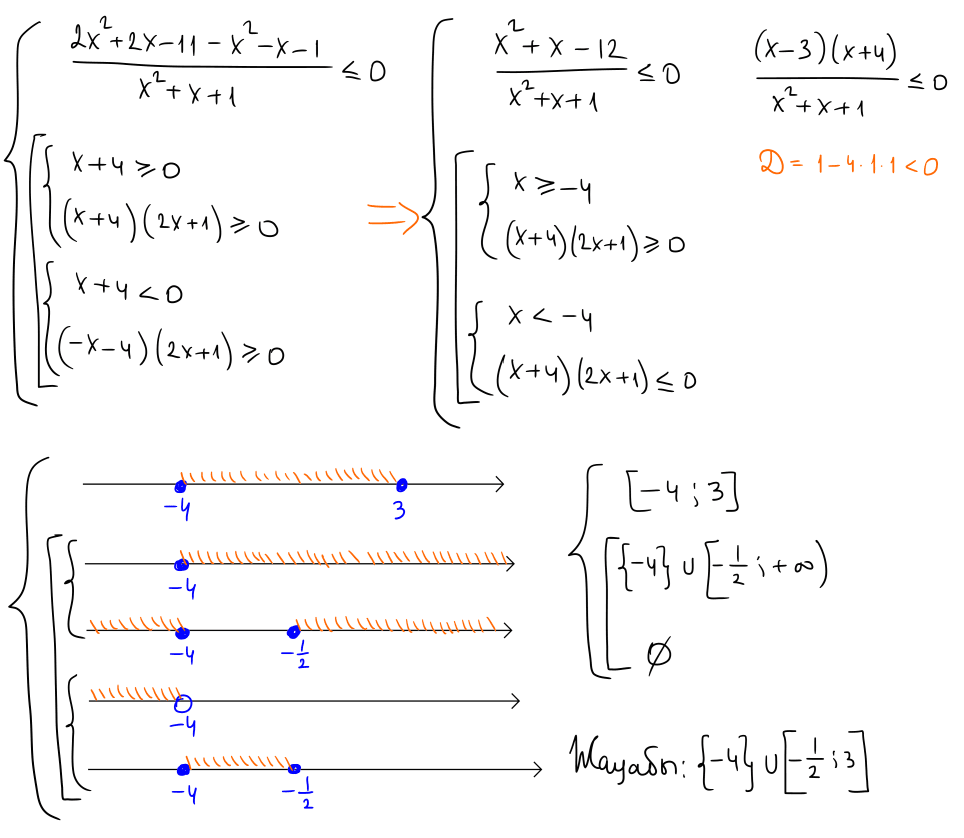
№ 10 Теңсіздікті шешіңіз: $\left\{\begin{array}{l}\dfrac{2 x^2+2 x-11}{x^2+x+1} \leq 1 \\ |x+4| \cdot(2 x+1) \geq 0\end{array}\right.$

№ 11 Теңсіздікті шешіңіз: $\dfrac{1}{|x-9|} \leq \dfrac{x-3}{4 x-11}$

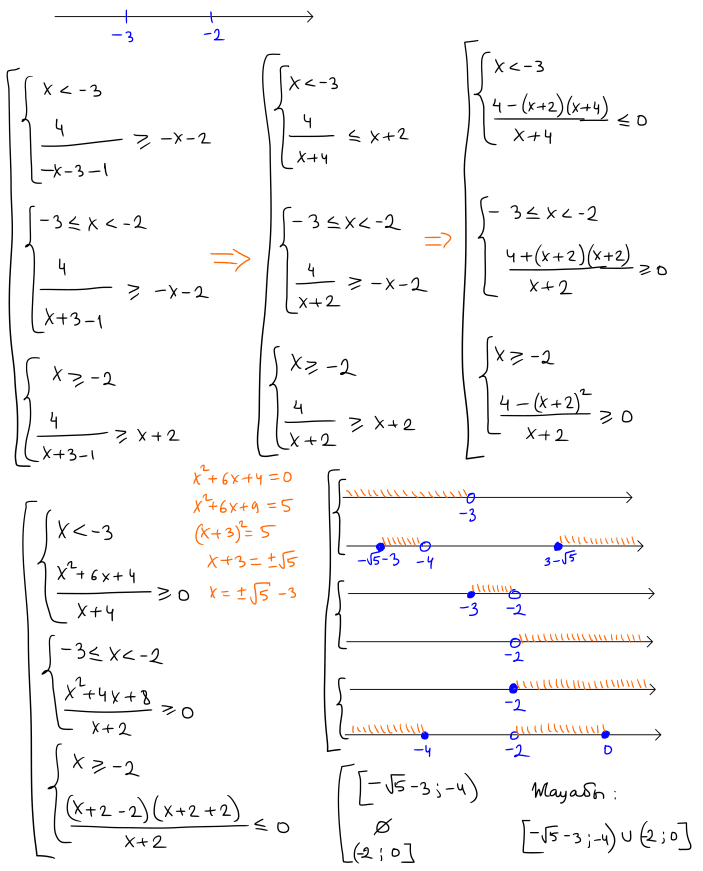
№ 12 Теңсіздікті шешіңіз: $\dfrac{4}{|x+3|-1} \geq|x+2|$

№ 13 Теңсіздікті шешіңіз: $1\lt 3^{\left|x^2-x\right|}\lt 9$

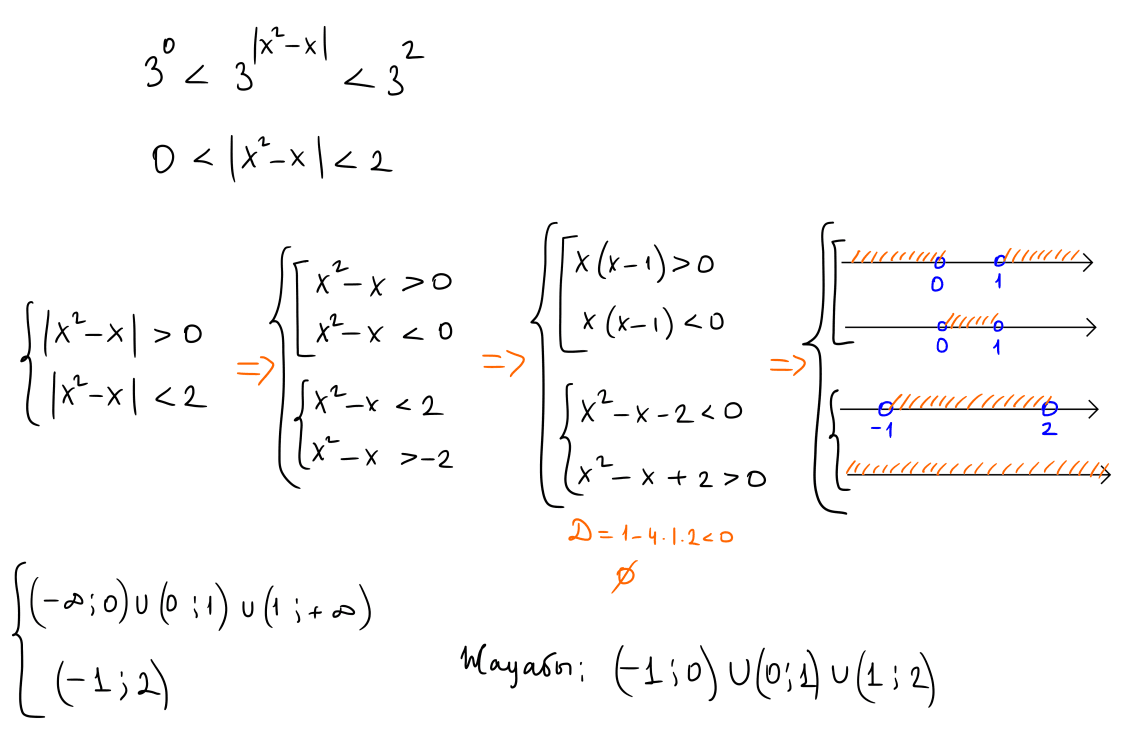
№ 14 Теңсіздікті шешіңіз: $\left|2^{2 x}-3 \cdot 2^x+2\right|\gt \left|4^x-3 \cdot 2^x-10\right|$

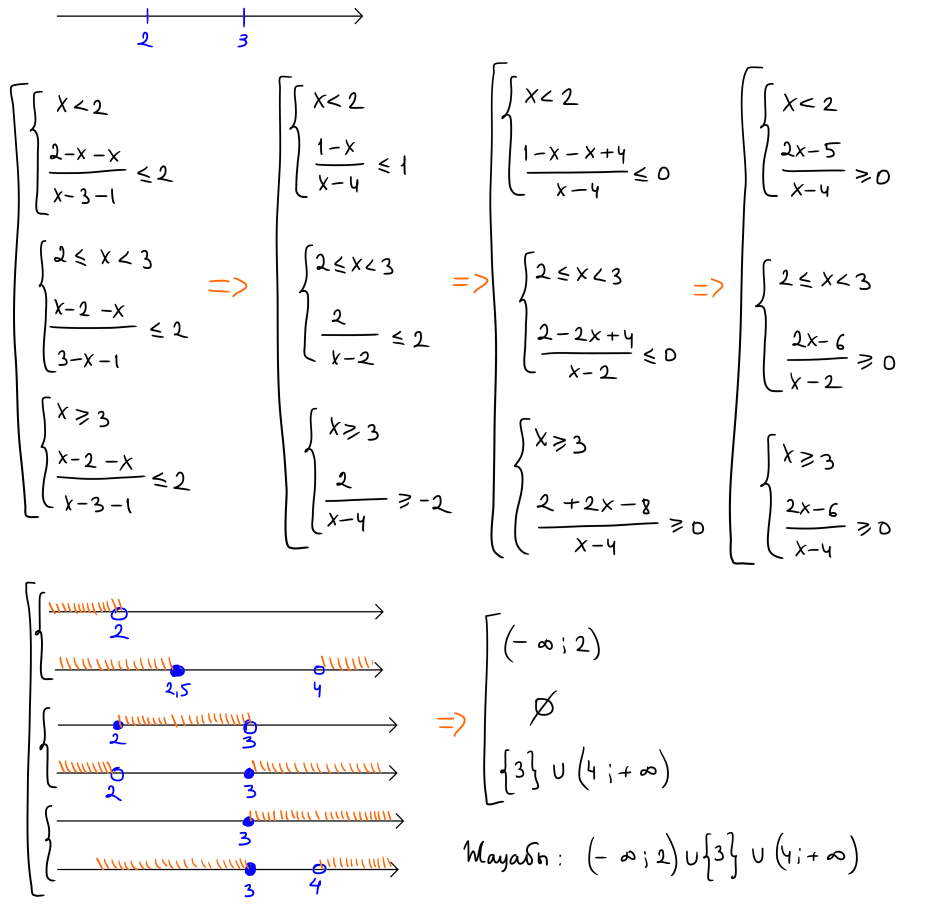
№ 15 Теңсіздікті шешіңіз: $\dfrac{|2-x|-x}{|x-3|-1} \leq 2$

№ 16 Теңсіздікті шешіңіз: $\dfrac{|x+3|-1}{4-2|x+4|} \geq-1$

№ 17 Теңсіздікті шешіңіз: $|x| \cdot\left(x^2-2 x-3\right) \geq 0$

№ 18 Теңсіздікті шешіңіз: $\frac{1}{|x|}\left(x^4-6 x^2-16\right) \leq 0$

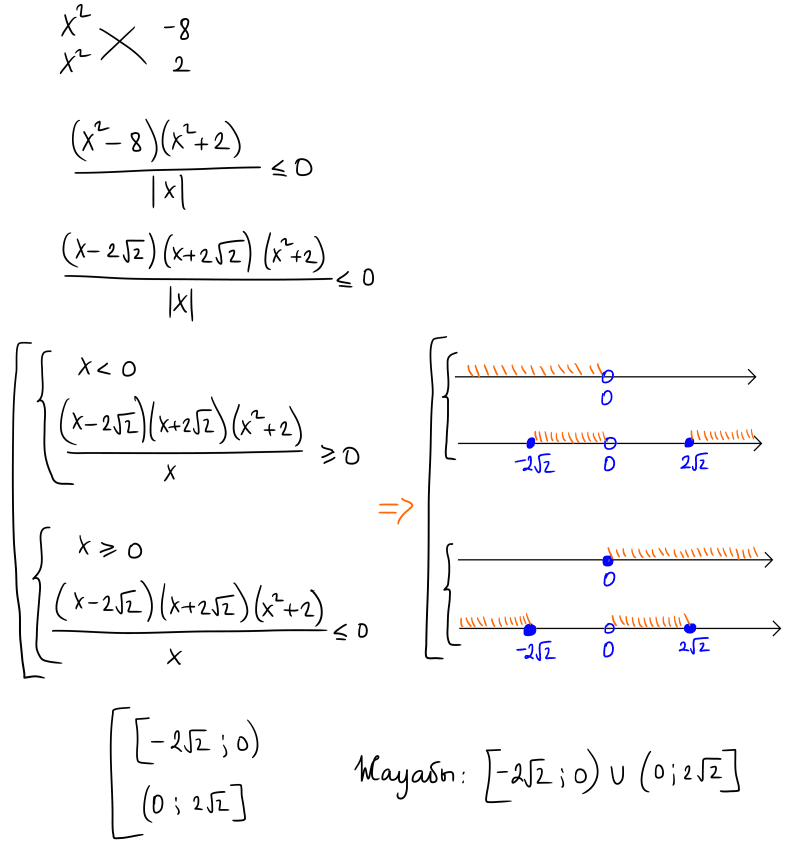
№ 19 Теңсіздікті шешіңіз: $\left|x^2-1\right|\lt x^2-|x|+1$

№ 20 Теңсіздікті шешіңіз: $\left(2-x+x^2\right)^{0,5} \leq|x-3|$